磁耦合电路
TIP
互感:电感对临近电感产生感应电压降的能力;自感:电感自身的电感量
- 线圈
和 临近,在线圈 上施加电流 , 则线圈 自身的电压降为 ,同时因 留经电流后产生的磁通量有部分耦合到线圈 ,线圈 上会产生感应电压降 ,其中 定义为线圈1对线圈2的互感系数; - 同样,有线圈2对线圈1的互感系数
,因互易性, 与线圈的形状、几何位置、空间媒质有关,与线圈中的电流无关(电感 也与流经的电流无关) 值始终为正,但 值可正可负 - 只有变化的电流才能产生互感电压
- 耦合系数定义:
- 线圈
同名端:电感的绕向影响感应电压的方向,为了解决这个问题,引入同名端的概念
当两个电流分别从两个线圈的对应端子同时流入或流出,若所产生的磁通相互加强时,则这两个对应端子称为两互感线圈的同名端;
电流从线圈1的同名端流进,线圈2的感应电压﹢定义在同名端,则
值为正,否则 值为负,如下所示 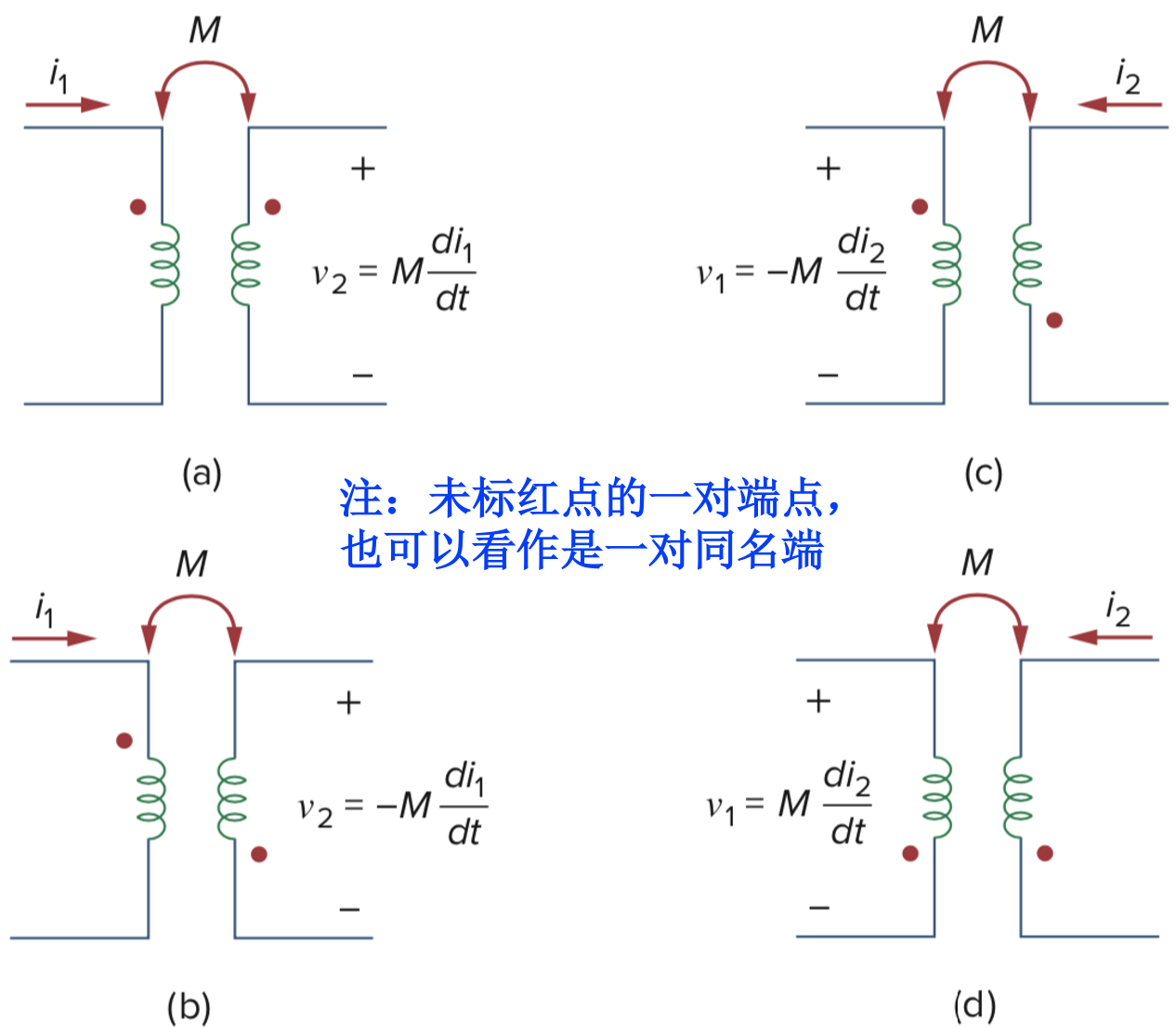
顺接串联等效电感:
反接串联等效电感:
同侧并联等效电感:
,也可以用等效电路理解:
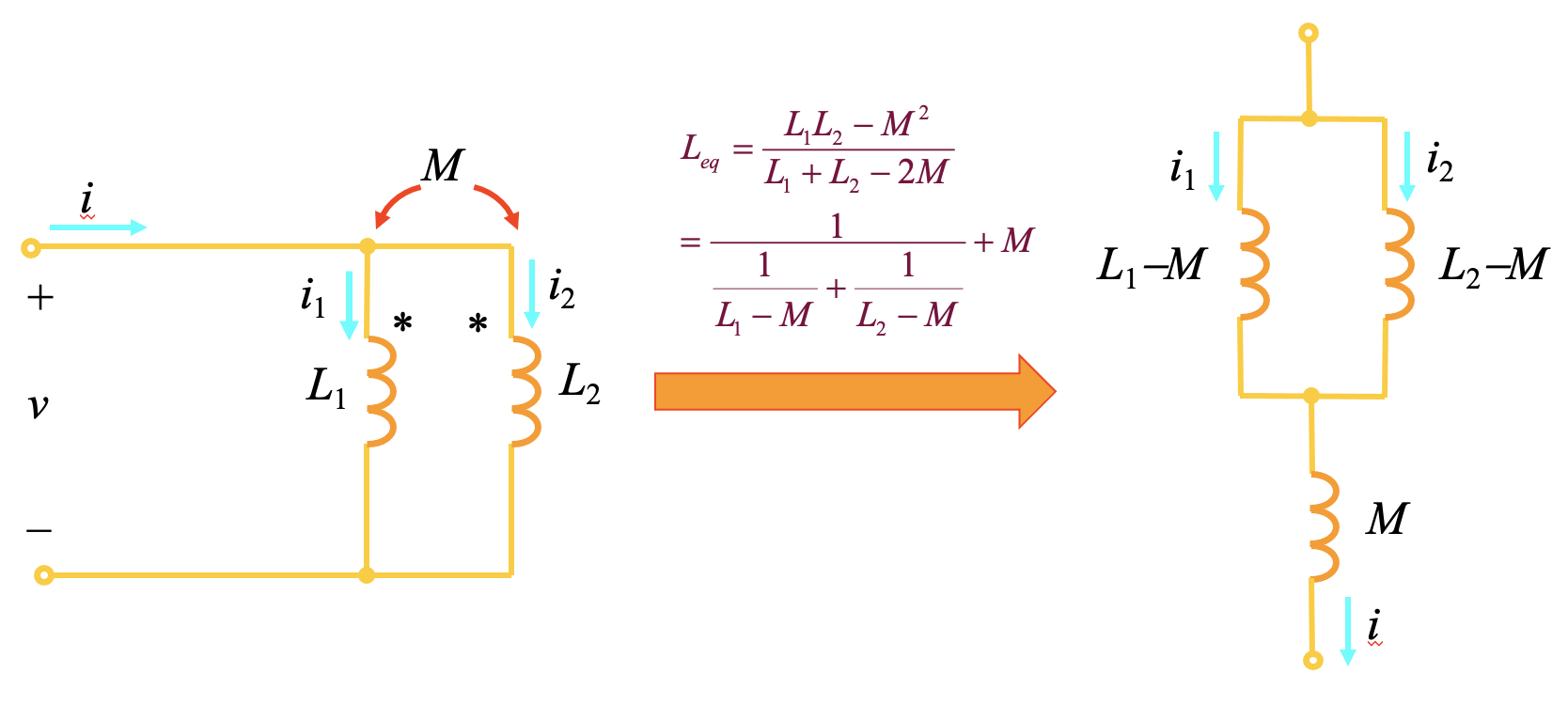
- 异侧并联等效电感:
,即,异侧并联相当于 用 替代 - 若非串并联,需要单独分析流经每个电感的电流对其他电感的贡献,同名则增强,非同名则减弱
互感耦合电路的分析
去耦方法,如上面同名端定义所述,电流从同名端流入,则在另一侧相应的同名端同向串联感应电压源
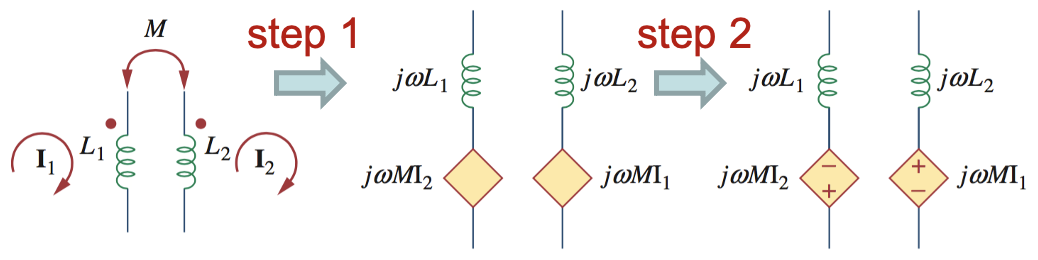
理想变压器
理想变压器的三个理想化条件:无损耗、全耦合、自感和互感值无限大(用匝数比替代互感电路的自感互感值)
理想变压器的电压电流约束关系如下,注意①电压﹢定义在同名端;②电流对同名端“一进一出”,同时满足①和②则比值为正,否则比值为负
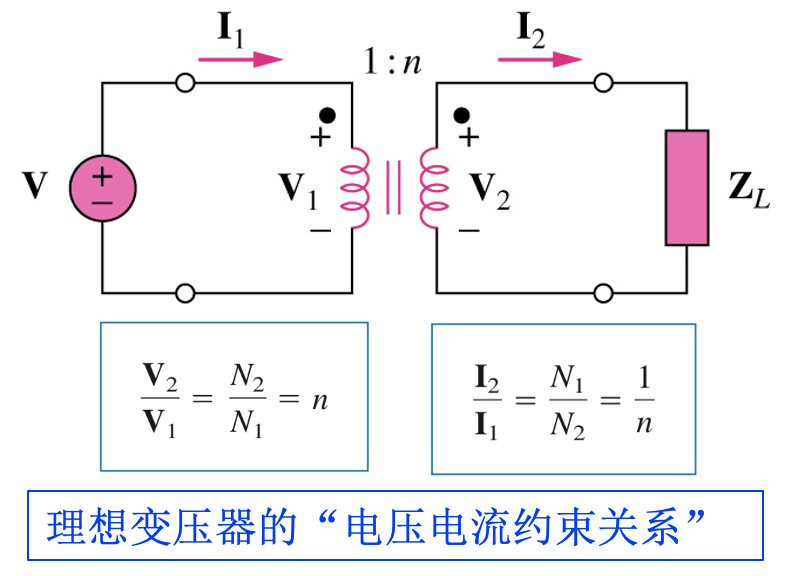
阻抗变换:按匝数比的平方缩放,
习题及参考解答
知识点1: 互感概念及计算
1、下图所示存在互感的电感串联后的总电感是 ________ 。
A.
C.
2、下图所示串联电路中的互感元件的耦合系数为 ________ 。
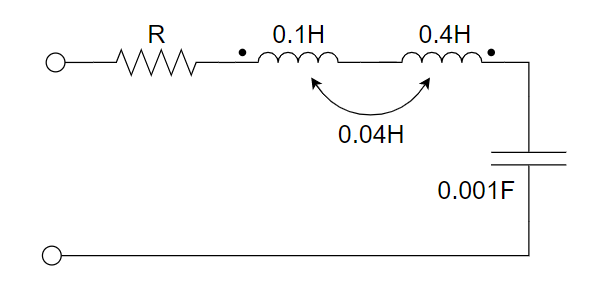
3、两互感线圈的耦合系数
A.
4、两互感线圈同侧并联时,其等效电感量为 ________ 。
A.
5、两互感线圈的电感量分别为 0.5 H 和 2 H ,耦合系数
6、如右图所示电路,电流
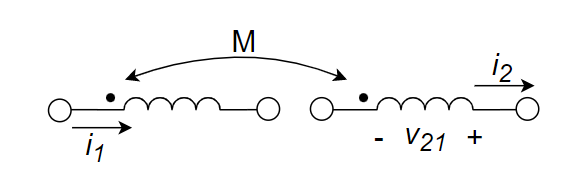
A.
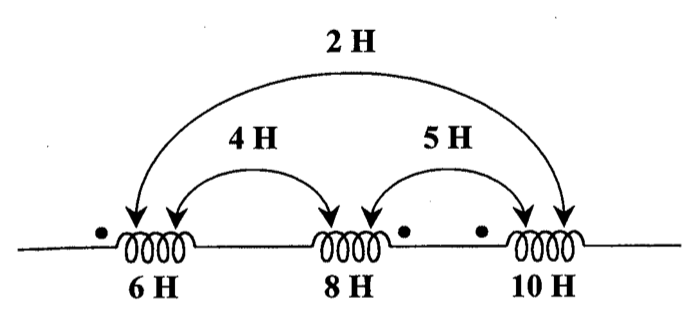
7、计算如下3个串联电感的去耦总电感.
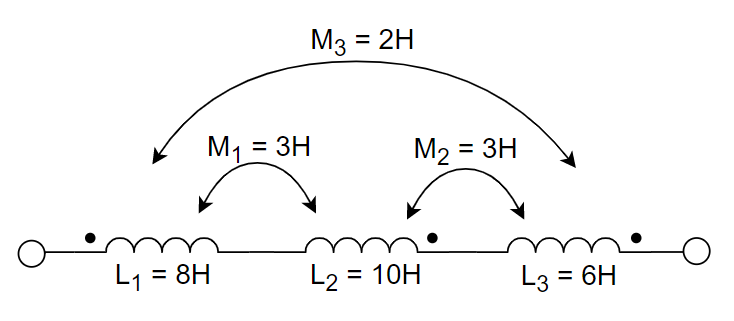
8、两个存在互感的线圈的耦合系数与 ________ 无关。
A. 线圈的形状 B. 线圈的几何位置
C. 线圈中流过的电流 D. 线圈的空间媒质
9、已知
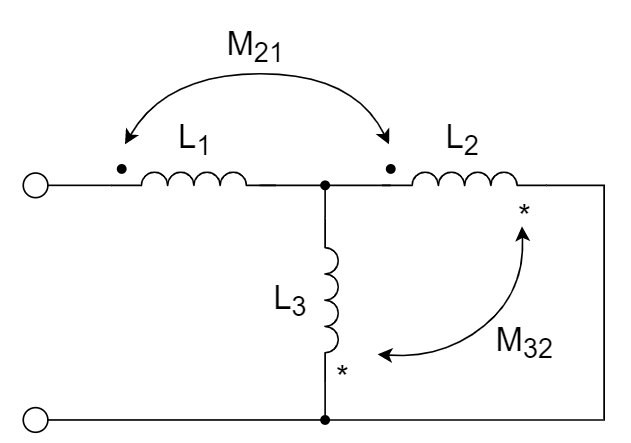
10、求下图的等效电感
参考解答
A
0.2
B
A
0.8H
A
解:
与 , 与 不是同名端, 与 互为同名端 那么三个串联电感的总电感量为:
C
解:
在端口施加一外接正弦信号
,为上正下负;设两个小回路的电流分别为 和 ,为顺时针方向。 列网孔电流方程如下
代入计算得到:
, 因此该端口电路的等效电感为
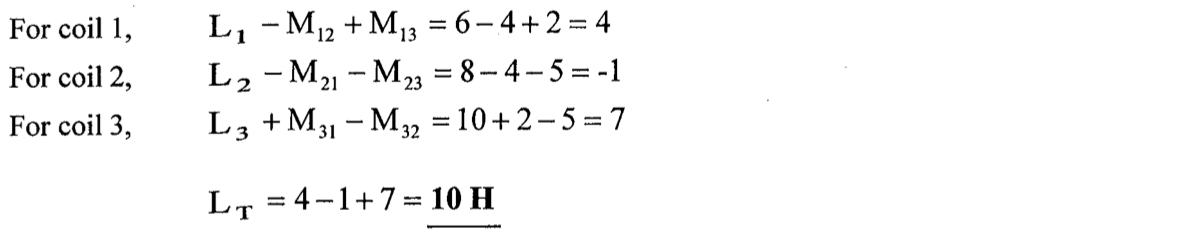
知识点2: 同名端的判别
1、下图所示电路中同名端为 ________ 。
A.(A、B、C) B.(B、Y、C) C.(A、Y、Z) D.(A、B、Z)
参考解答
- C
知识点3:含变压器电路的分析计算
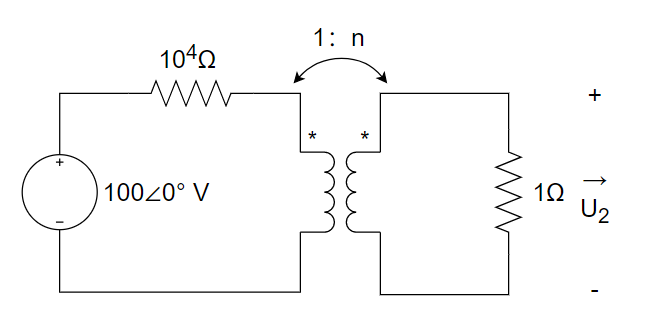
1、电路如下图所示。
①试选择合适的匝数比使传输到负载上的功率达到最大;
②求1Ω负载上获得的最大功率。
2、右图所示电路ab端的输入阻抗为 ________ 。
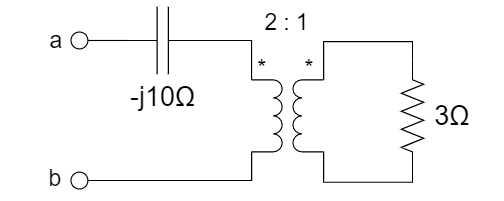
A. 12 - j10 (Ω) B. 12 (Ω)
C. 10 - j12 (Ω) D. - j10 (Ω)
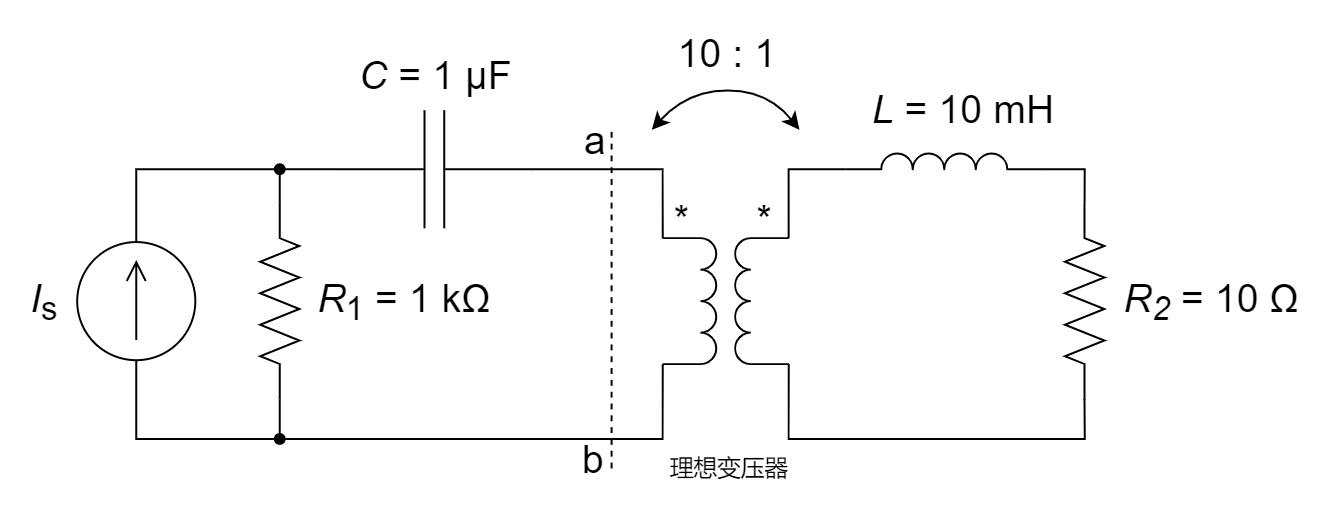
3、理想变压器次级线圈上的阻抗如下图所示,若正弦电流源为
(1) 从ab端看变压器二端的等效阻抗;
(2) 电阻
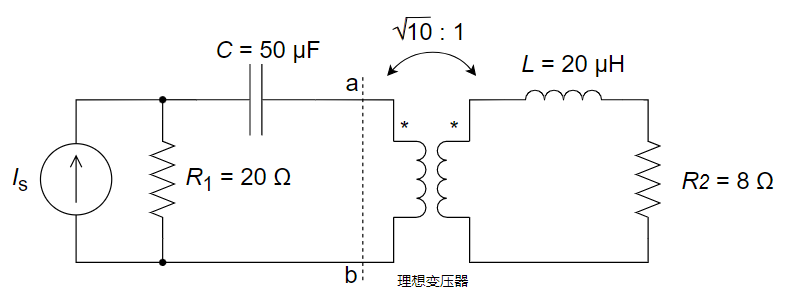
4、对于理想变压器,根据下图所示电流电压方向,正确的关系为 ________ 。
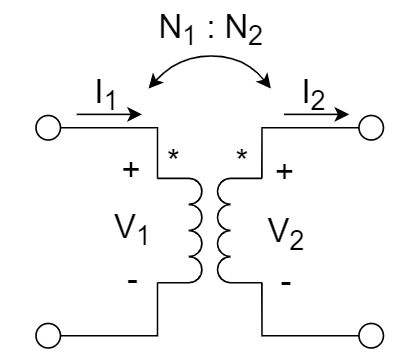
A.
C.
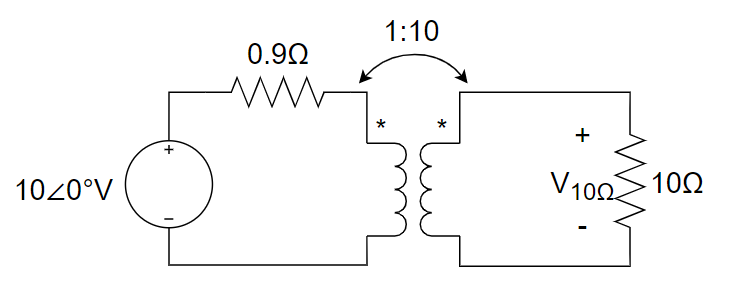
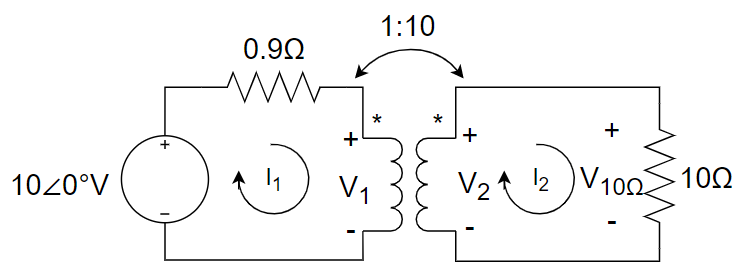
5、如下图包含理想变压器的电路中,求 10 Ω 电阻上的电压
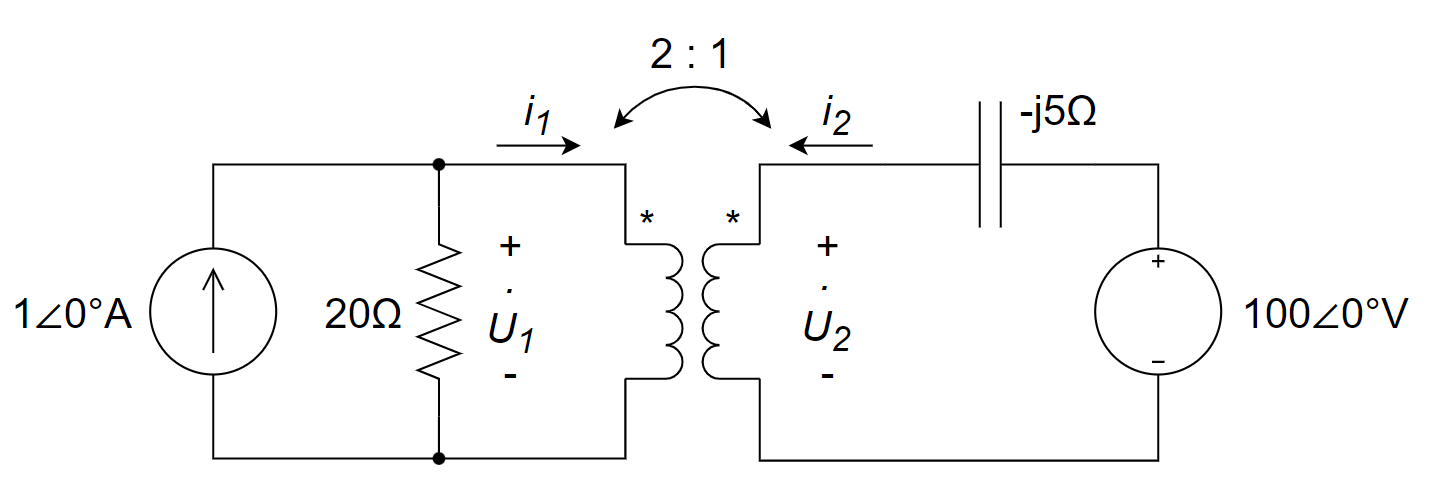
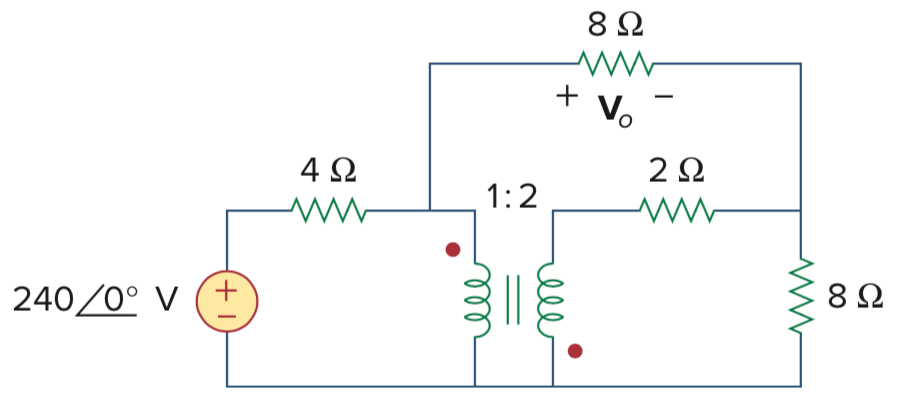
6、见下图所示的正弦稳态电路,用叠加定理求电压相量
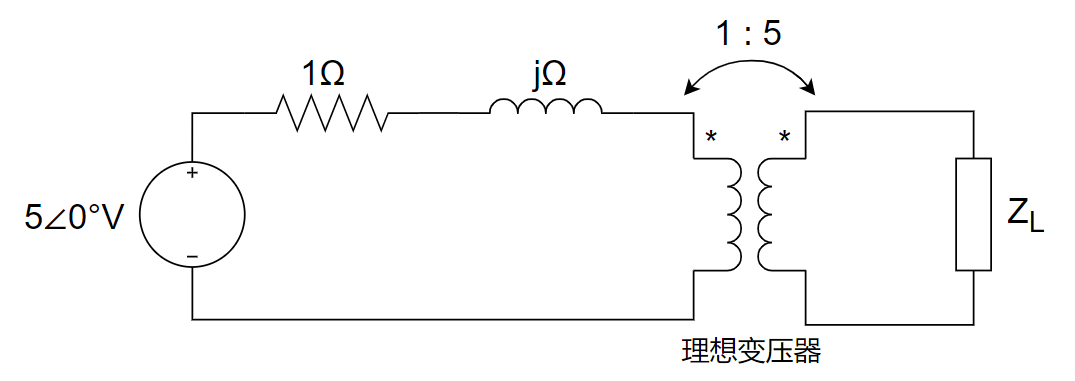
7、见下图所示电路,负载阻抗为何值时其输出功率最大,最大功率为多少?
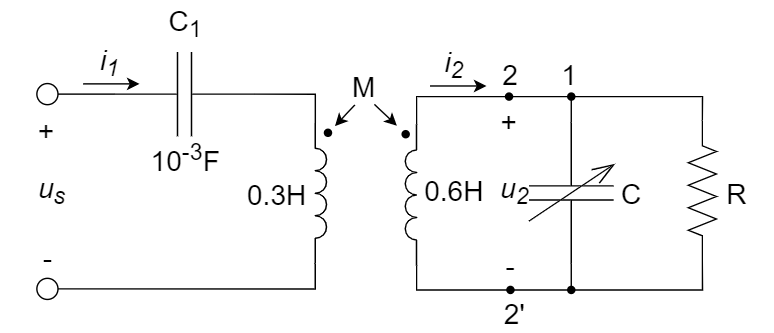
8、已知一个正弦交流电源的开路电压
9、已知下图所示电路中
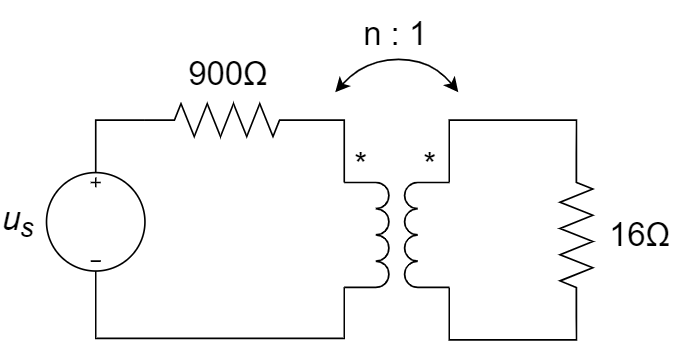
10、如下图中所示电路,欲使 16 Ω负载获得最大功率,则其中理想变压器的匝数比应为 ________ 。
11、下面理想变压器电路中,求
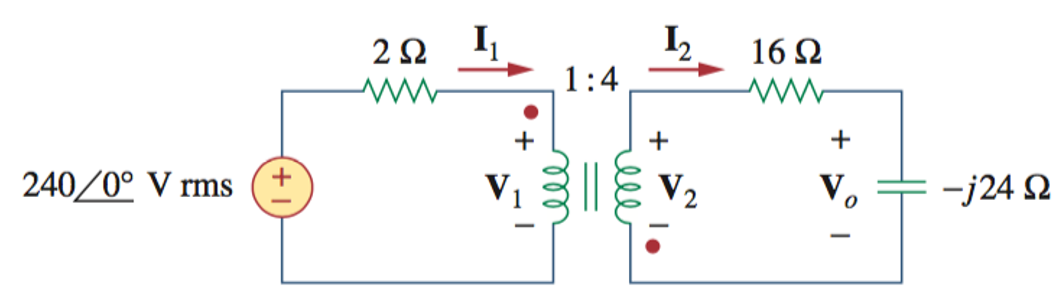
12、求下面电路中的
13、如下图所示电路,若正弦电流源为
(1) 从ab端向右看的等效阻抗;
(2) 流过电阻
参考解答
解:
方法一:
设
和 , 和 ,则有: 解得
方法二:
根据阻抗变换,
时获得最大功率传输; 理想变压器不损耗功率,所以
A
(a)
(b)
A
解:
(1) 方法一:
对于回路1:
对于回路2:
对于理想变压器,有:
解得:
故而
(1) 方法二:
将次级负载折算到初级线圈,求出初级电流为 10A ,然后根据理想变压器电压电流比例关系,写出 V~10Ω~ = 10 V。
解:
电流源单独作用时:
电压源单独作用时:
解:
根据最大功率传输定理,
当
时,负载的输出功率最大 此时
(从负载侧算);也可以从源测算 解:
因为理想变压器不消耗能量,所以电源输给变压器的功率就等于负载吸收的功率。
当理想变压器入端电阻
时,负载吸收最大功率。 根据变压器的阻抗变换公式
即理想变压器匝数比
时,负载获得的功率最大。 此时变压器原线圈电流
通过负载的电流
负载端电压
解:
端口 2 - 2' 用电压源
替代,则网孔方程
解得:
诺顿等效电路的参数为:
显然,在电路端口 2 - 2‘ 并联接入 RC 电路后,端电压
最大时,R 获最大功率,其实现条件为
此时,
, 全部流入 R,其最大功率应当为
只有当
为感性时,才有实现的可能。 7.5
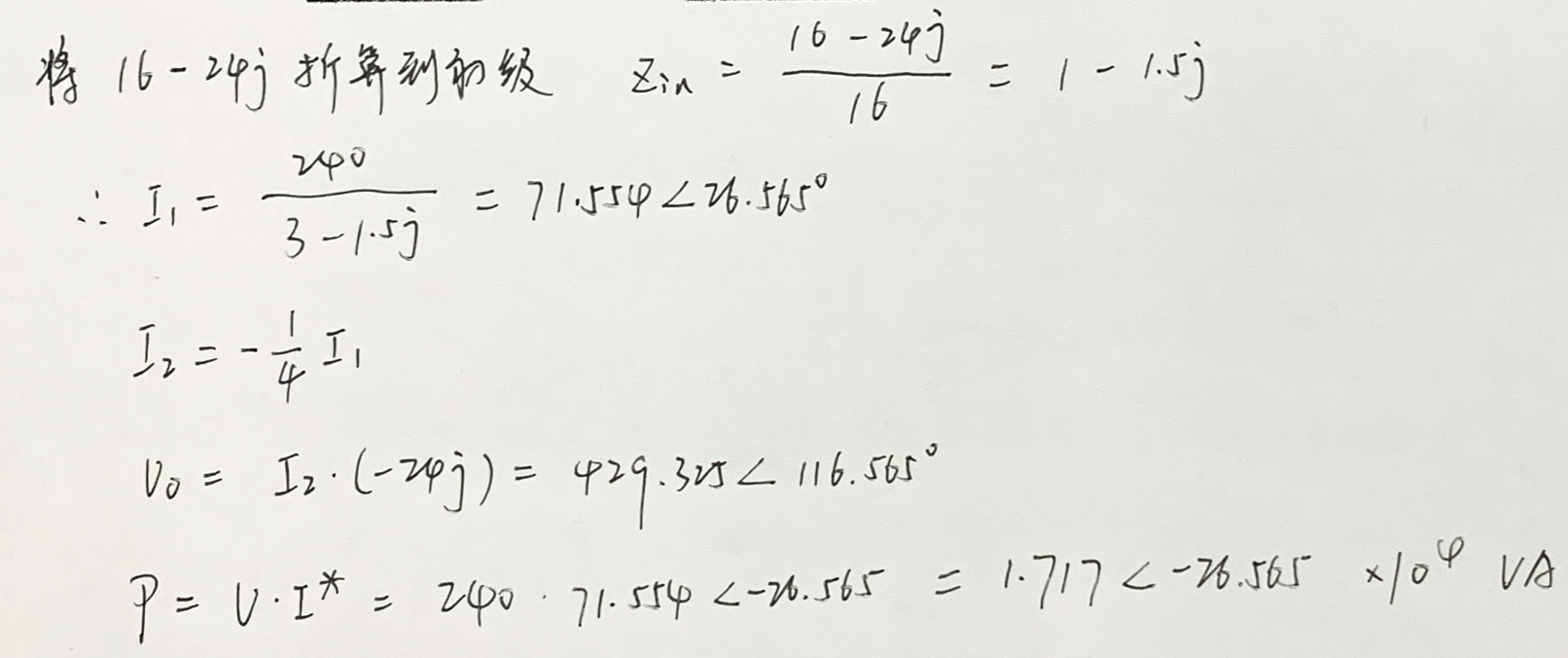

解:
(1)
(2)
知识点4: 互感耦合电路的分析
1、用网孔电流法列下图所示电路的回路方程,线圈
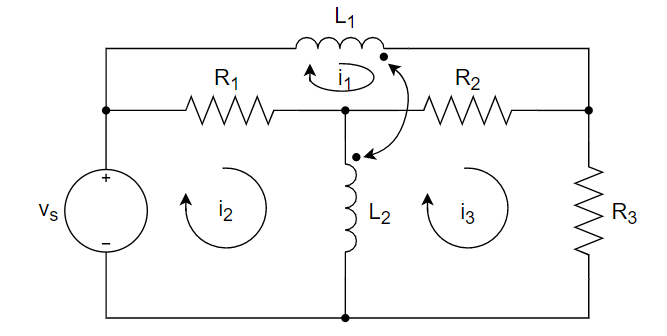
2、列写下图所示电路的网孔电流方程。
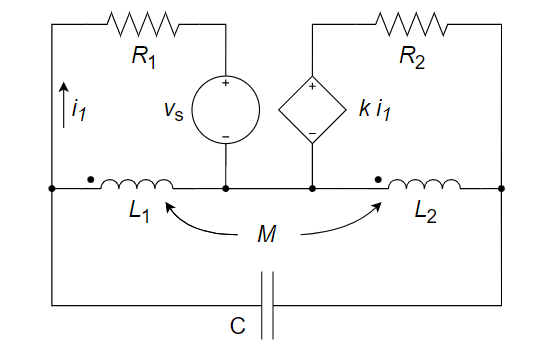
3、右图所示电路中的输出电压
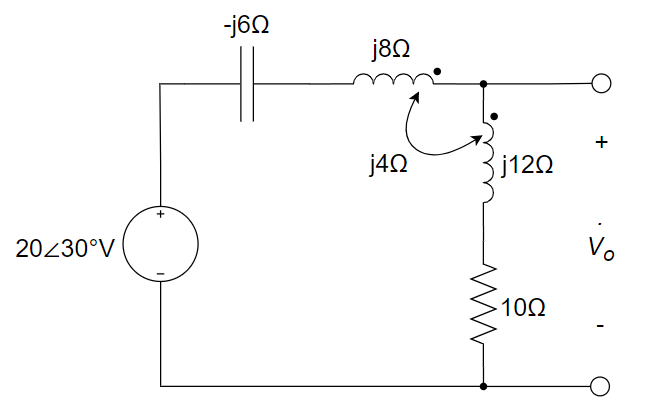
4、在下图所示电路中,已知
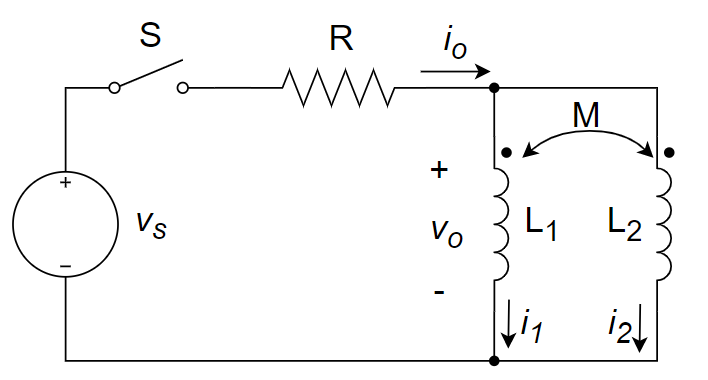
5、用网孔电流法求如下电路中的支路电流
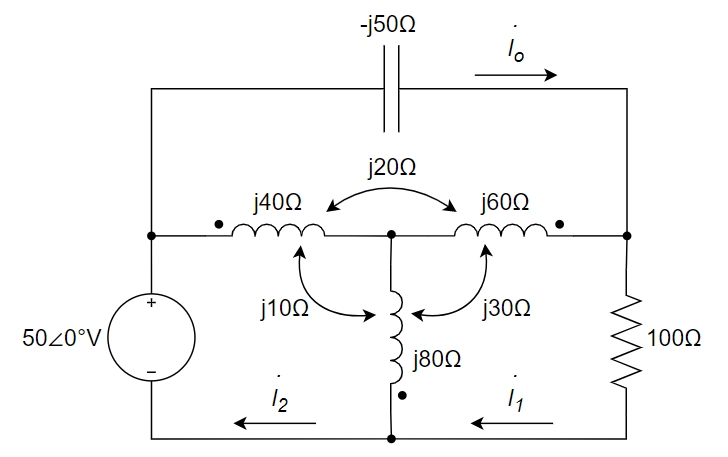
6、求下图中
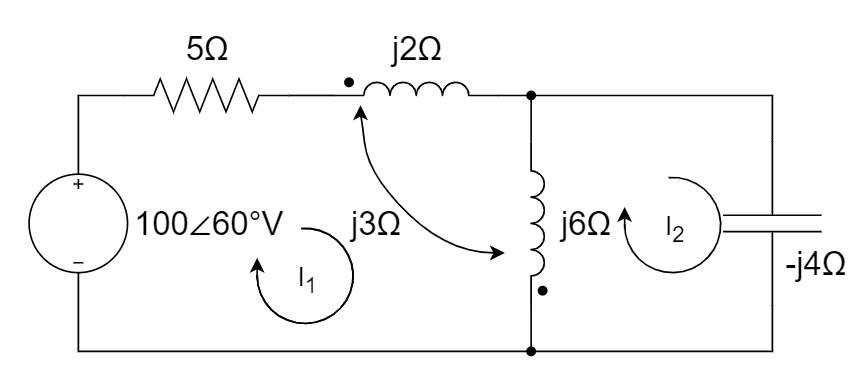
7、电感耦合电路如图所示。
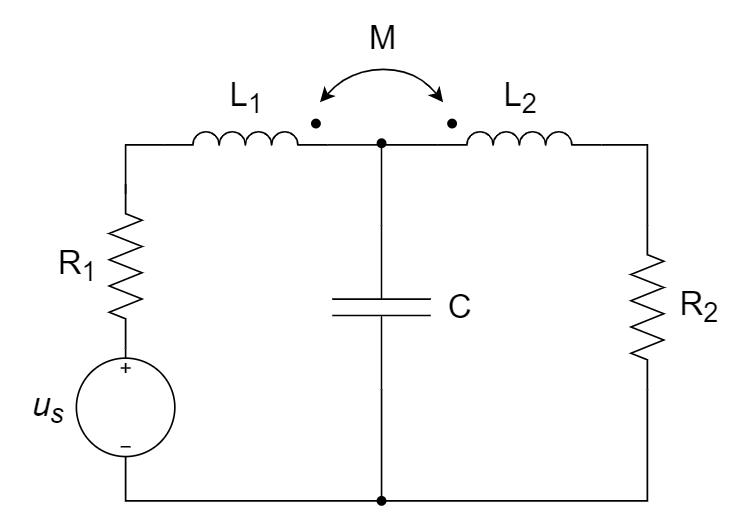
8、求耦合系数,以及
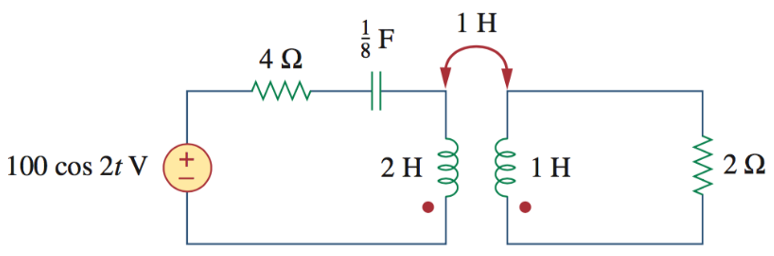
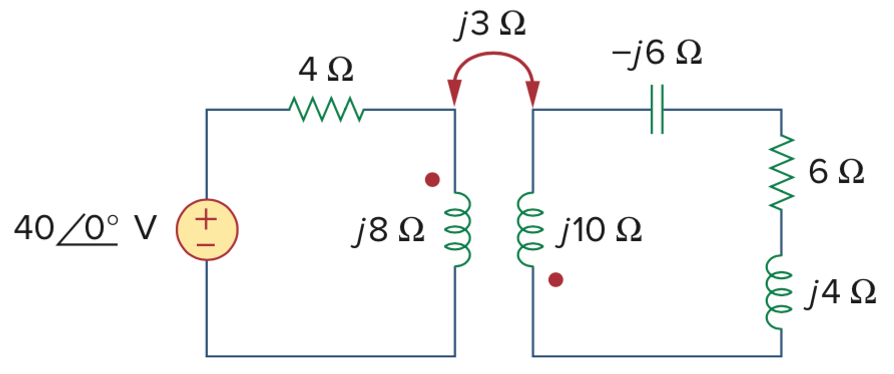
9、求以下电路的输入阻抗(从电压源往右看的阻抗)和流过电压源的电流
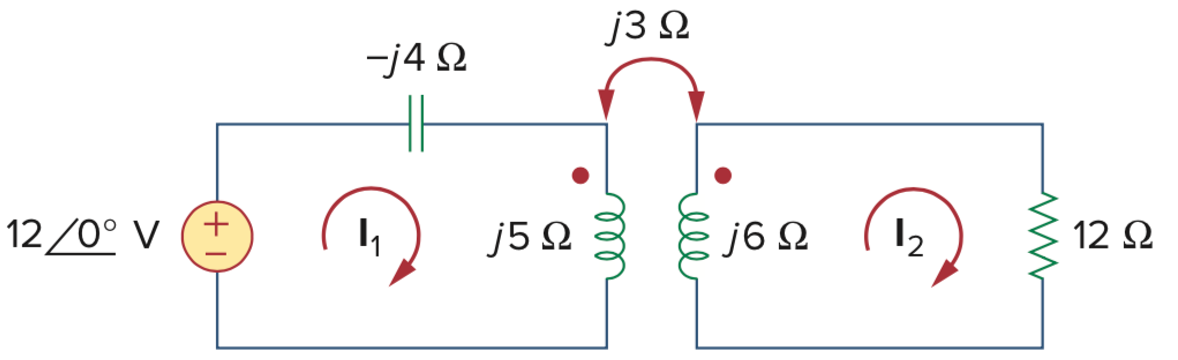
10、用 T 型等效模型化简电路,求
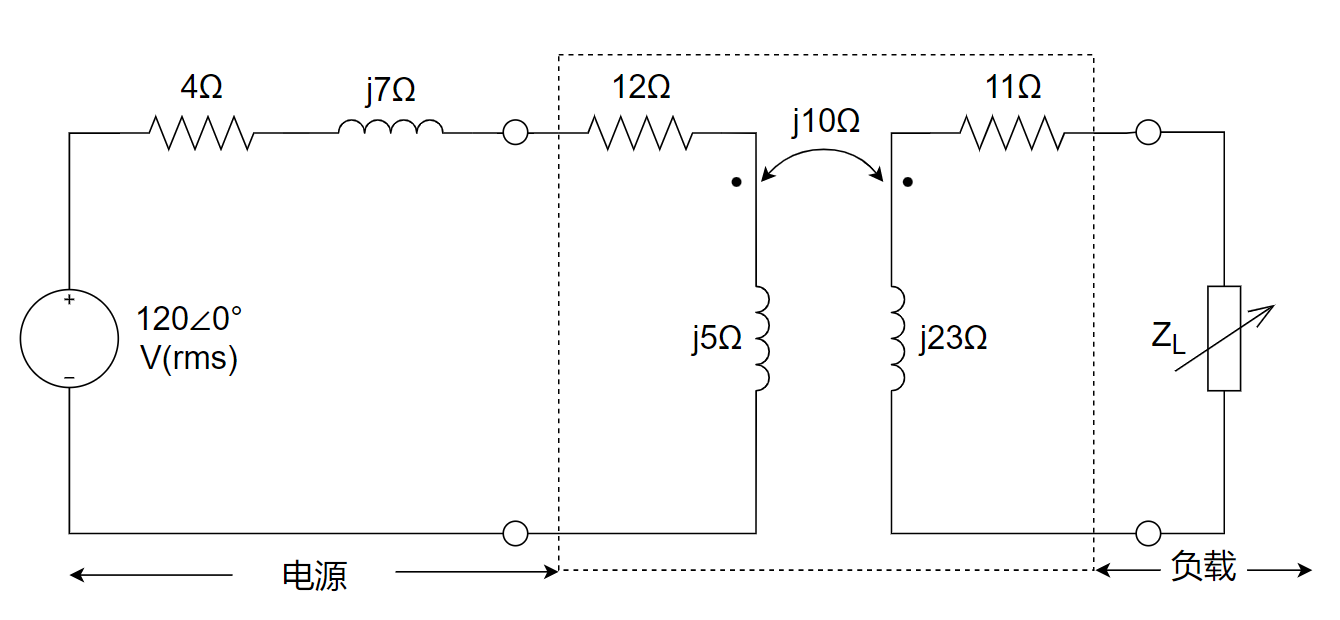
11、调整下图所示电路的负载阻抗
参考解答
解
列网孔电流方程如下:
解:
设三个网孔的电流分别为
、 和 ,电流方向为顺时针方向。 列网孔电流方程如下:
21.962∠37.7° V
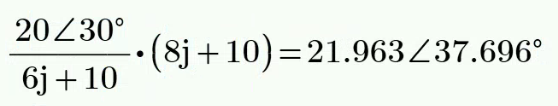
解:
根据题意
等效去耦电感
通解
,根据初始条件,可得 特解
故有
根据 KVL 可得:
由电路有
得
根据 KCL,
由于
,得: 解:
得出:
解:
列网孔电流方程如下
解得:
解:
设两回路的电流依次为
和 ,列网孔电流方程如下 其中,
电源提供的有功功率为
解得:
电源提供的有功功率为

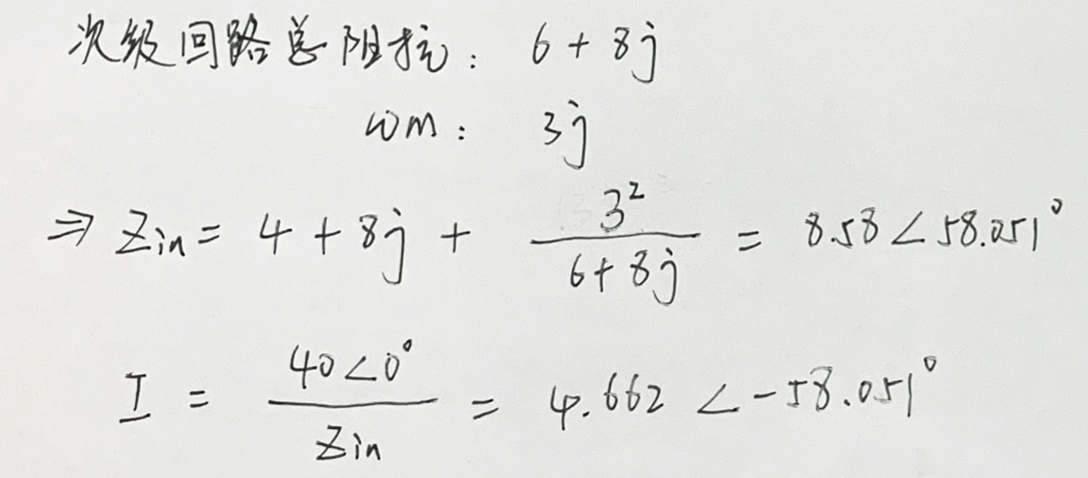
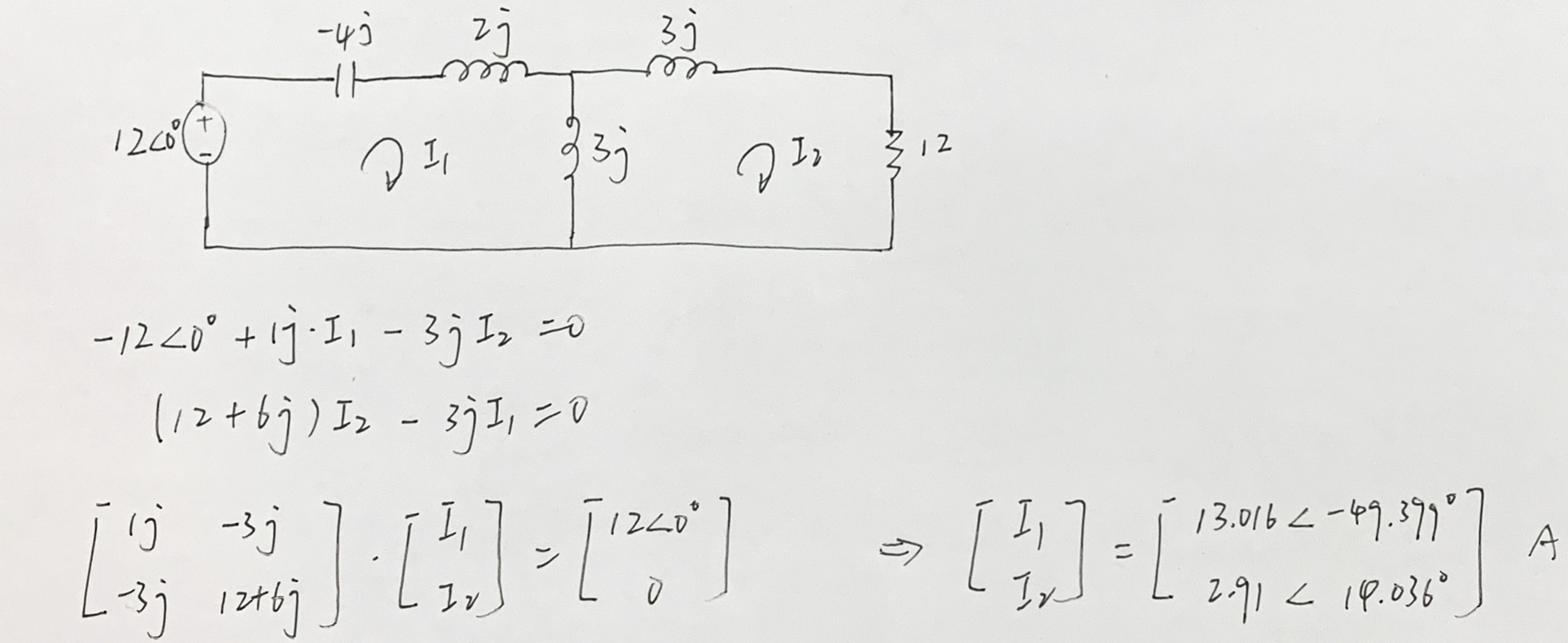
解:
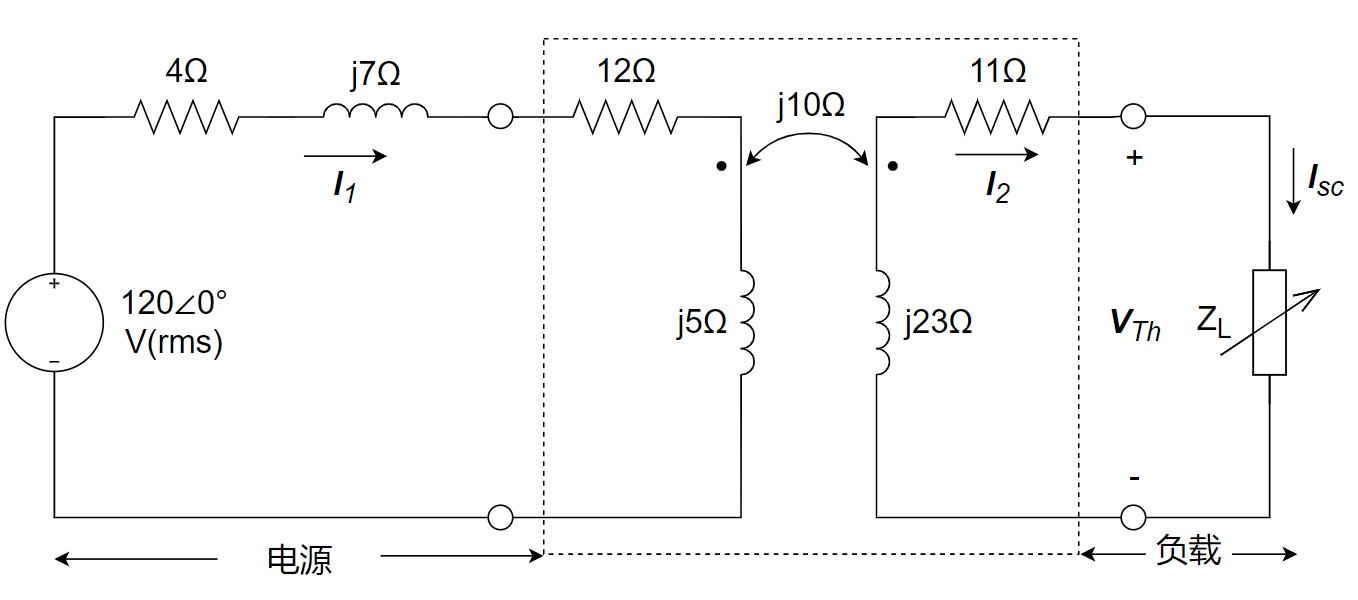
负载短路:
解得:
因此,
知识点5: 其他
1、以下对于理想变压器的描述,________ 是不正确的。
A. 输入功率等于输出功率 B. 互感和自感系数无穷大
C. 初级电流随次级电流增大而减小 D.能同时改变交变信号的电压和电流
2、理想变压器初级与次级的匝数比
参考解答
- C
- 1:10 10:1