Fundamentals of Electronic Circuits

Appearance

过渡过程的经典解法 ​

TIP

  1. 动态电路和过渡过程的概念：

    • 电感、电容的“电压电流约束关系”与时间 t 有关，所以电感、电容又称为动态元件，含电感、电容的电路也被称为动态电路；

    • 动态电路的一个特征是：当电路结构发生变化时（一般通过“开关”的切换来实现），可能使电路从原来的工作状态，转变到一个新的工作状态，这种转变往往需要一定的时间，这一过程被称为动态电路的过渡过程；

    • 开关切换的动作也被称为“换路”，一般认为换路是在 时刻进行的，把换路前的最终时刻记为 ，把换路后的最初时刻记为 ;

    • 分析动态电路的方法：根据KCL、KVL、元件的电压电流约束关系，写出微分方程，并求解；这一方法在时域中进行，称为经典解法；

      image-20220905214609711

  2. 一阶电路的响应、二阶电路的响应；

    • 一阶电路：化简后的电路仅含一个储能元件
    • 解一阶微分方程需要知道变量初始值
    • 时刻的电路状态由 时刻的电路状态获得，且基于
      • 电感电流不能突变
      • 电容电压不能突变
    • 一阶电路的衰减常数：, 或

  3. 零输入响应、零状态响应、全响应及其分解方式、三要素法分析；

    • 输入指 时刻，电路中有无电源； 状态指 时刻，电路中的储能元件有无初始储能

    • 零输入响应：无外加激励电源（零输入），仅由动态元件初始储能所产生的响应

    • 零状态响应：动态元件初始储能为零（零状态），由外加激励电源引起的响应

    • 实际情况往往是 时刻电源和初始储能都有的，即全响应

    • 三要素法：初始值、稳态值、时间常数；初始与稳态的差值随时间常数的指数衰减，所以

  4. 二阶电路的响应

    • 二阶电路：化简后的电路含两个储能元件

    • 解二阶微分方程需要知道变量初始值，以及变量导数的初始值

    • focus on 不能突变的量，即电感电流、电容电压，寻找变量初始值；变量导数的初始值由元件的外围电路决定

      • 如电感，求电流导数的初始值，因 ，需经由电感两端电压初始值获得
      • 如电容，求电压导数的初始值，因 ，需经由流经电容电流初始值获得

    • 求解二阶微分方程，即获得二阶电路的解

      • step 1: 求变量及变量导数的初始值
      • step 2: 求微分方程的特解，即变量的稳态响应
      • step 3: 时刻，turn off 独立源，求齐次微分方程的通解，即变量的瞬态响应
      • step 4: 写出非齐次微分方程的通解，即稳态响应和瞬态响应相加
      • step 5: 结合初始条件，求待定系数

    • 对于串联 RLC、并联 RLC 这两种特殊的二阶电路，可根据衰减常数和谐振频率直接写出解的表达式

      • 衰减常数，对于串联 RLC， ；对于并联 RLC，

      • 谐振频率，

      • 典型的二阶电路有过阻尼（）、临界阻尼（）、欠阻尼（）三个 cases；临界阻尼衰减最快；以下以电容电压为例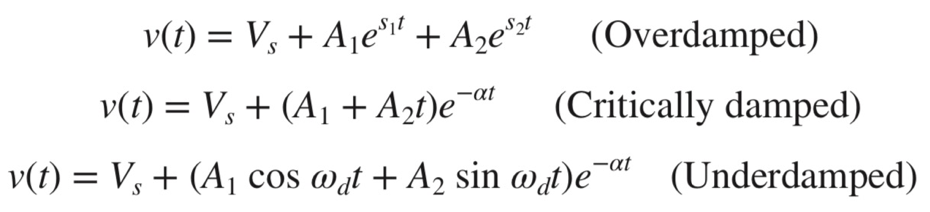

        image-20220905225258656

      • 选取电感电流还是电容电压作为变量？都可以。有激励时，取激励的量比较方便（即稳态时容易获得的是电压量还是电流量）；无激励时，并联取电压比较方便，串联取电流比较方便

  5. 阶跃响应、冲激响应。

    • 单位斜坡函数是单位阶跃函数的积分
    • 单位冲激函数是单位阶跃函数的导数
    • 一阶电路：单位冲激响应可当作电容两端初始电压为1/C （或流经电感的初始电流为1/L）的零输入响应来处理；
    • 二阶电路：冲激响应可以按阶跃激励的一阶导数求得

习题及参考解答 ​

知识点1： 一阶电路的响应 ​

1、已知电感无初始储能，开关 和 处于打开状态。t = 0 时开关 闭合，t = 0.2s 时开关 闭合，分别求两次换路后的电感电流 。

4-1-1

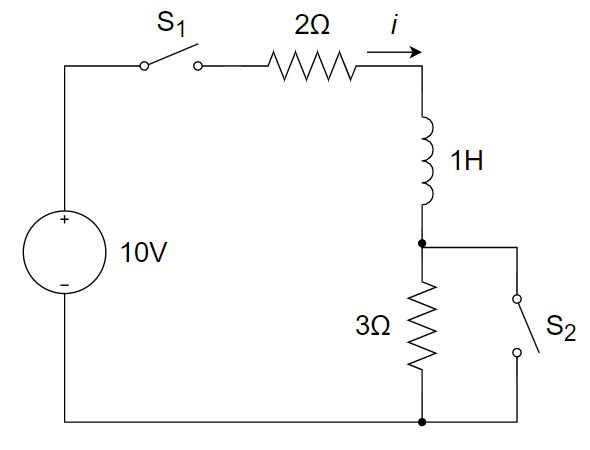
2、图示电路中开关断开时的电容电压 等于 ________ 。

4-1-2

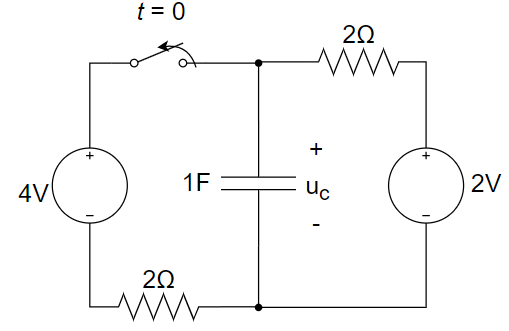
A. 2 V B. 3 V C. 4 V D. 0 V

3、如下图所示电路，开关 K 原长时间停留在位置 1，t = 0时转换到位置 2，求 和 。

4-1-3

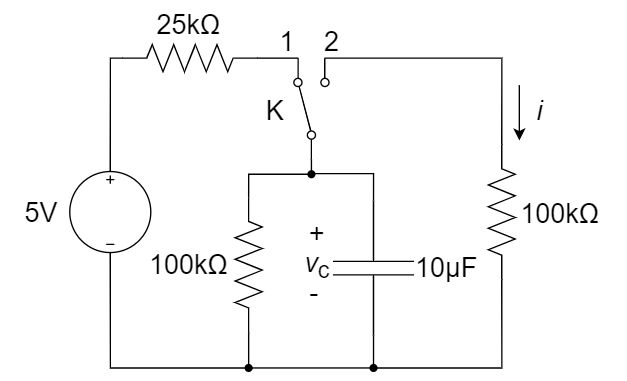
4、求下左图所示电路中电流 ，独立电压源的伏安特性曲线见下右图。

4-1-4-14-1-4-2

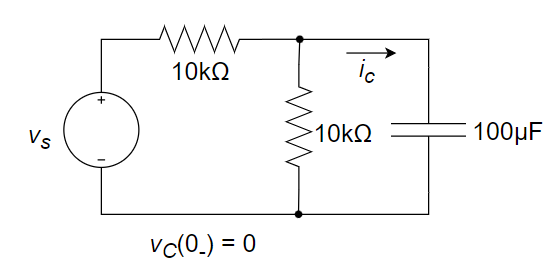
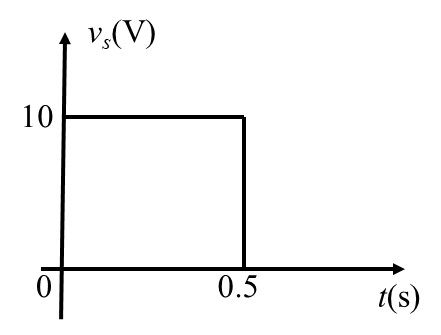
5、某 RL 一阶电路的全响应为 ，若初始状态不变，而输入电源幅度增加一倍，则全响应变为 ________ 。

A. B. C. D.

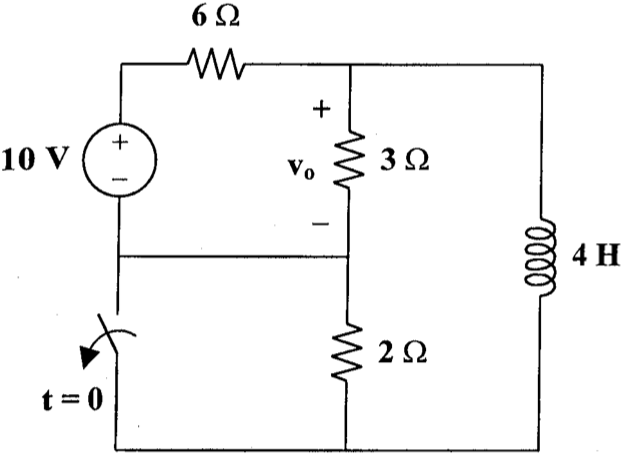
6、如下图所示电路，开关闭合时电路已进入稳态，在 t = 0 时刻开关打开，求 t > 0 时电流 的表达式。

4-1-6

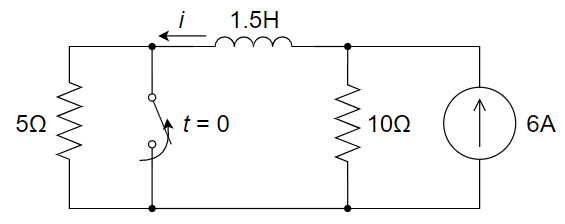
7、如下图所示电路，在 t = 0 时刻前，开关 S 在位置 1 时电路已达到稳定状态，t = 0 时开关由位置 1 合向位置 2，求 t ≥ 0 时的电压 。

4-1-7

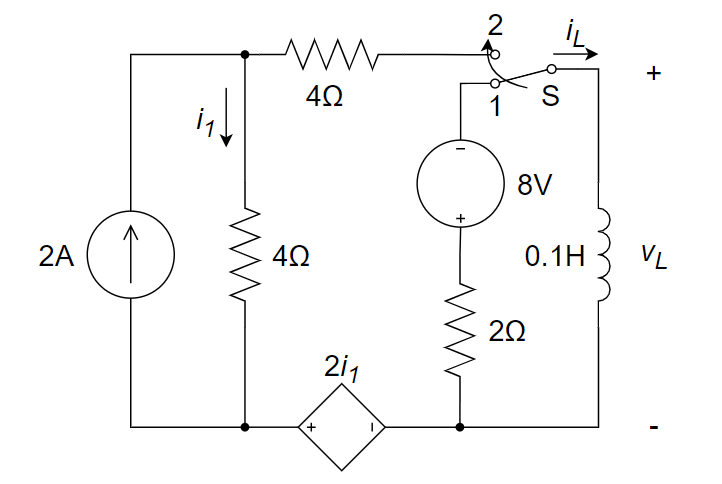
8、在下图所示电路中，电路换路前电容未储能，当 t = 0 时开关 S 闭合，求开关闭合后的 和 。

4-1-8

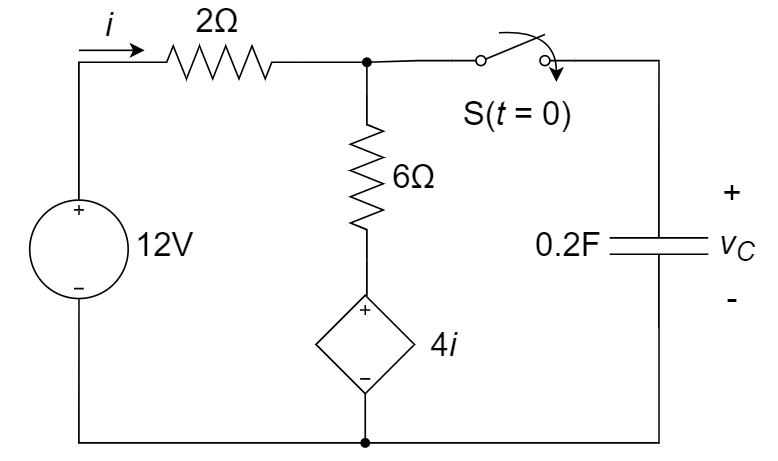
9、下图所示电路中， 时刻已经处于稳定状态，开关于 时闭合，则 时流过电感的电流为 ________ A。

4-1-9

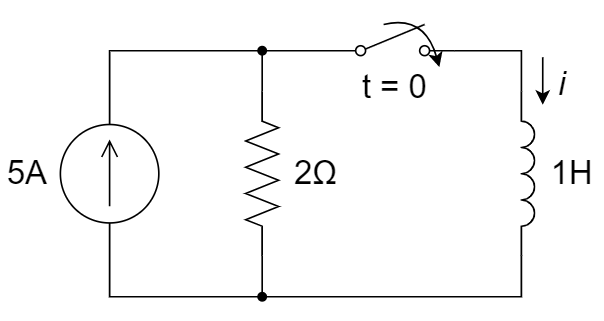
10、下图所示电路中，换路前电路已处于稳态，开关闭合后，支路电流 ________ 。

4-1-10

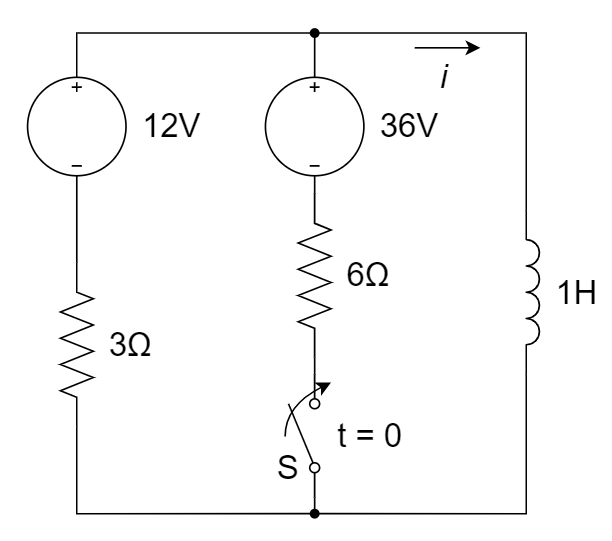
11、电路如图所示，开关已长时间处于 A 位置，t = 0 时刻转向 B 位置，求 t ≥ 0 时的 。

4-1-11

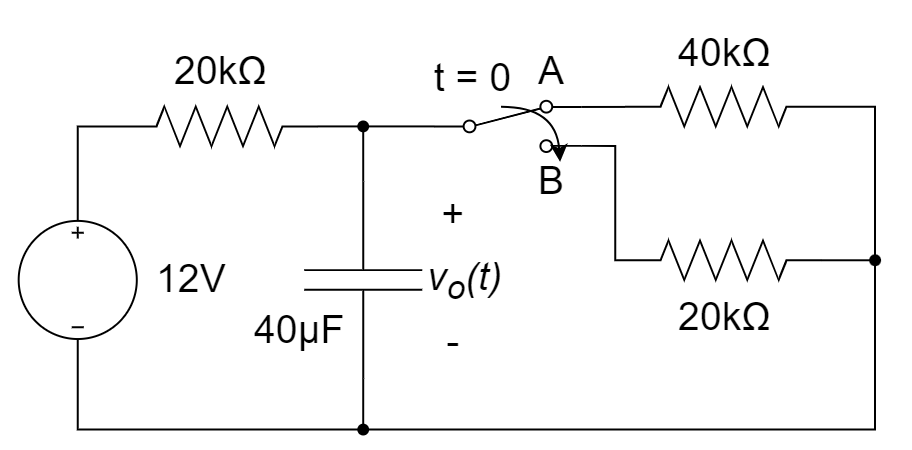
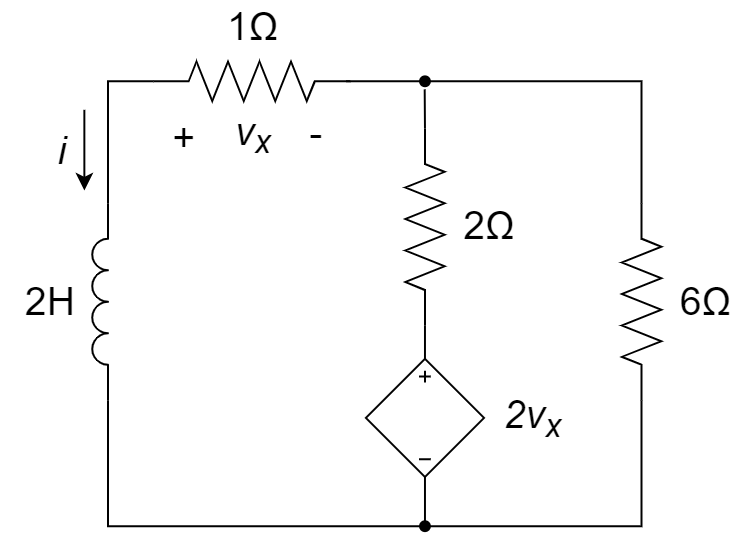
12、如图所示，若电感的初始电流 ，求 时刻的 和 。

4-1-12

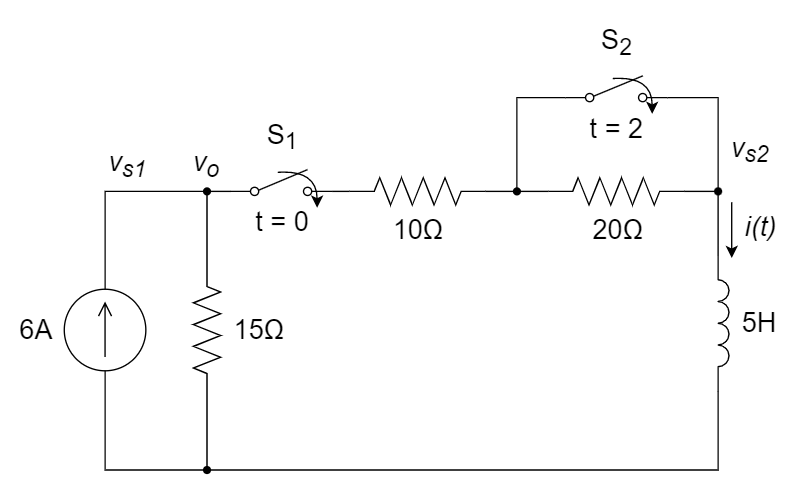
13、在下图中 时刻，S1、S2 开关是开启的； 开始，S1 开关关闭，但是 S2 开关在 时关闭，请计算通过电感的电流（可分段表示）。

4-1-13

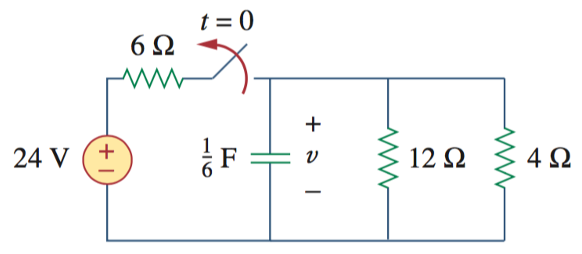
14、下图中，开关在 时刻断开，求 时的 和 时刻电容的储能

image-20221014155913169

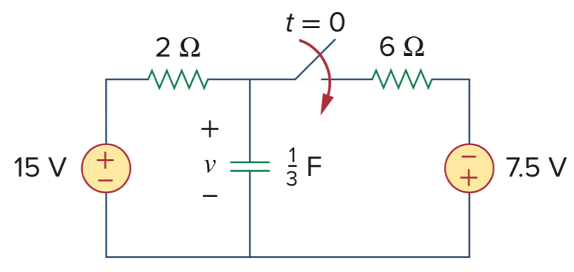
15、下图中，开关在 时刻闭合，求 时的 ，并计算 时刻的 值

image-20221014160351448

16、下图中，开关在 时刻闭合，求全时刻的 和

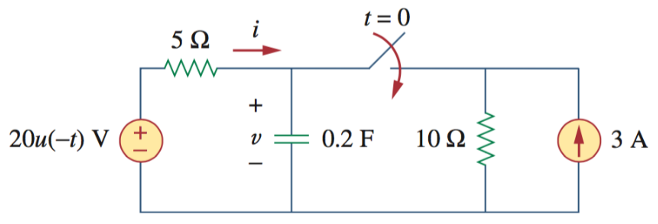
image-20221014160624696

17、下图中， A，求

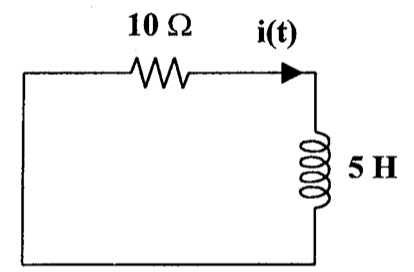
image-20221016172953025

18、下图中， V，求 和

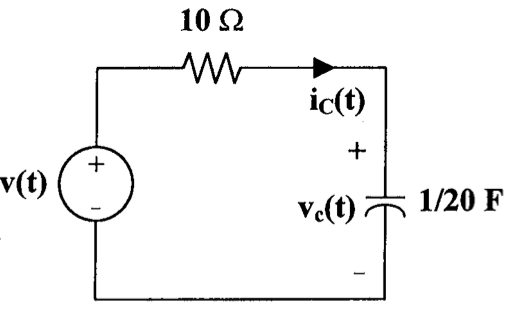
image-20221016173342705

19、下图中， V，求

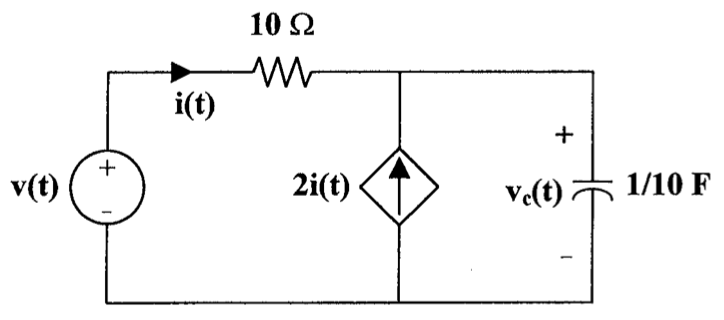
image-20221016173613176

20、下图中， V，求 和

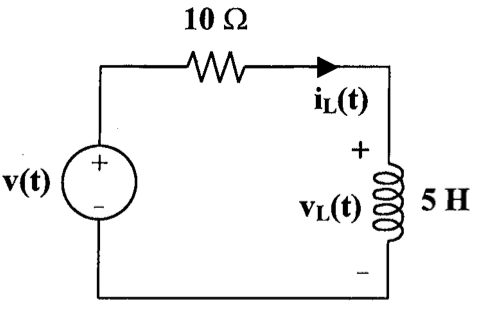
image-20221016173831777

21、下图中，求 时刻的

image-20221016174038018

参考解答

  1. 解：

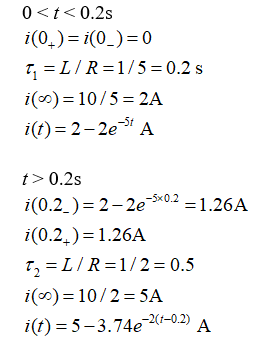
    image-20220906082513777

  2. B

  3. 解：

    开关在位置 1 时，可解得：

    ​

    ​ 时转换到位置 2 后，从电容两端看进去的等效电阻为

    ​

    ​

    因此，可得：

    ​

    ​

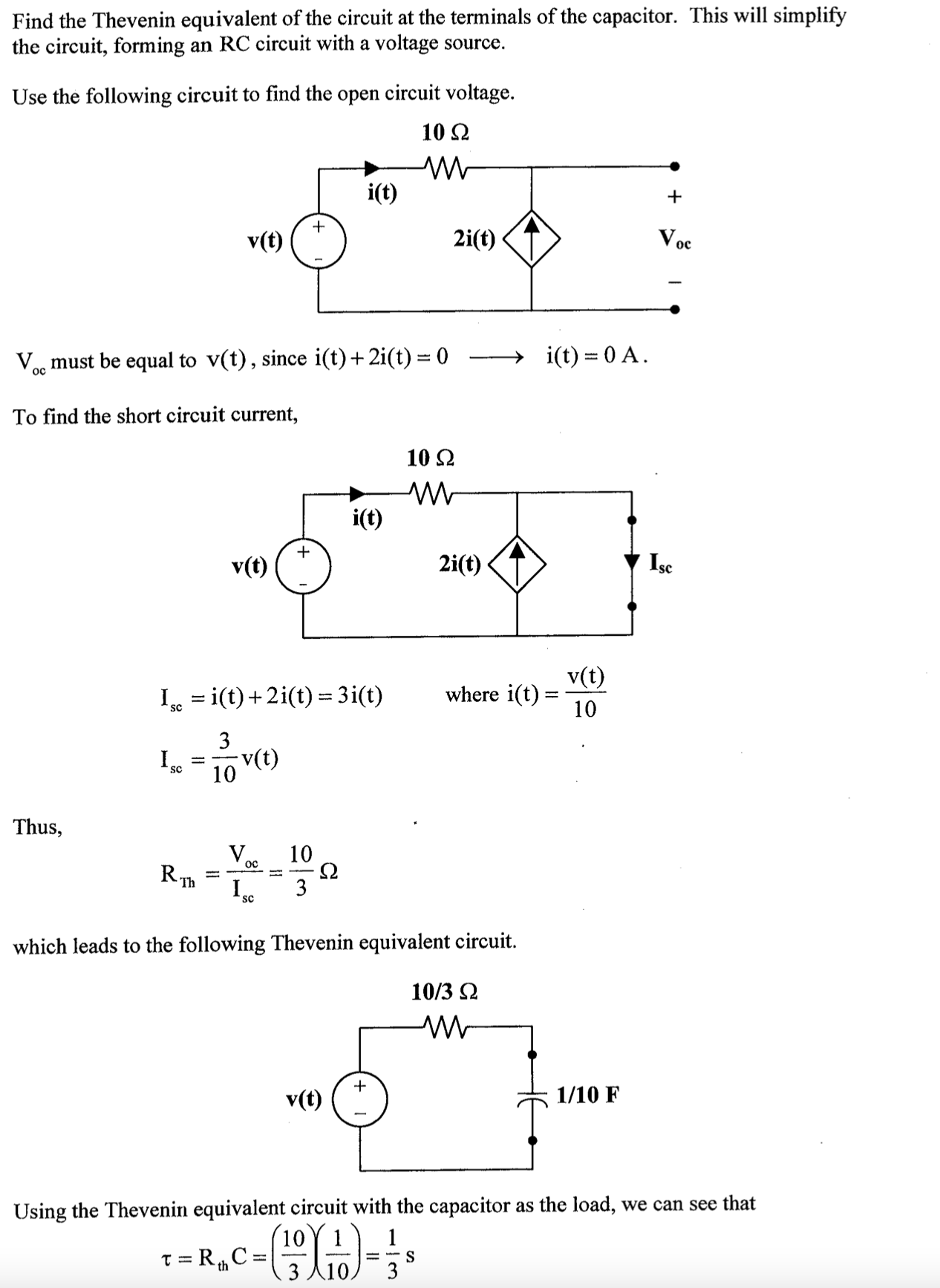
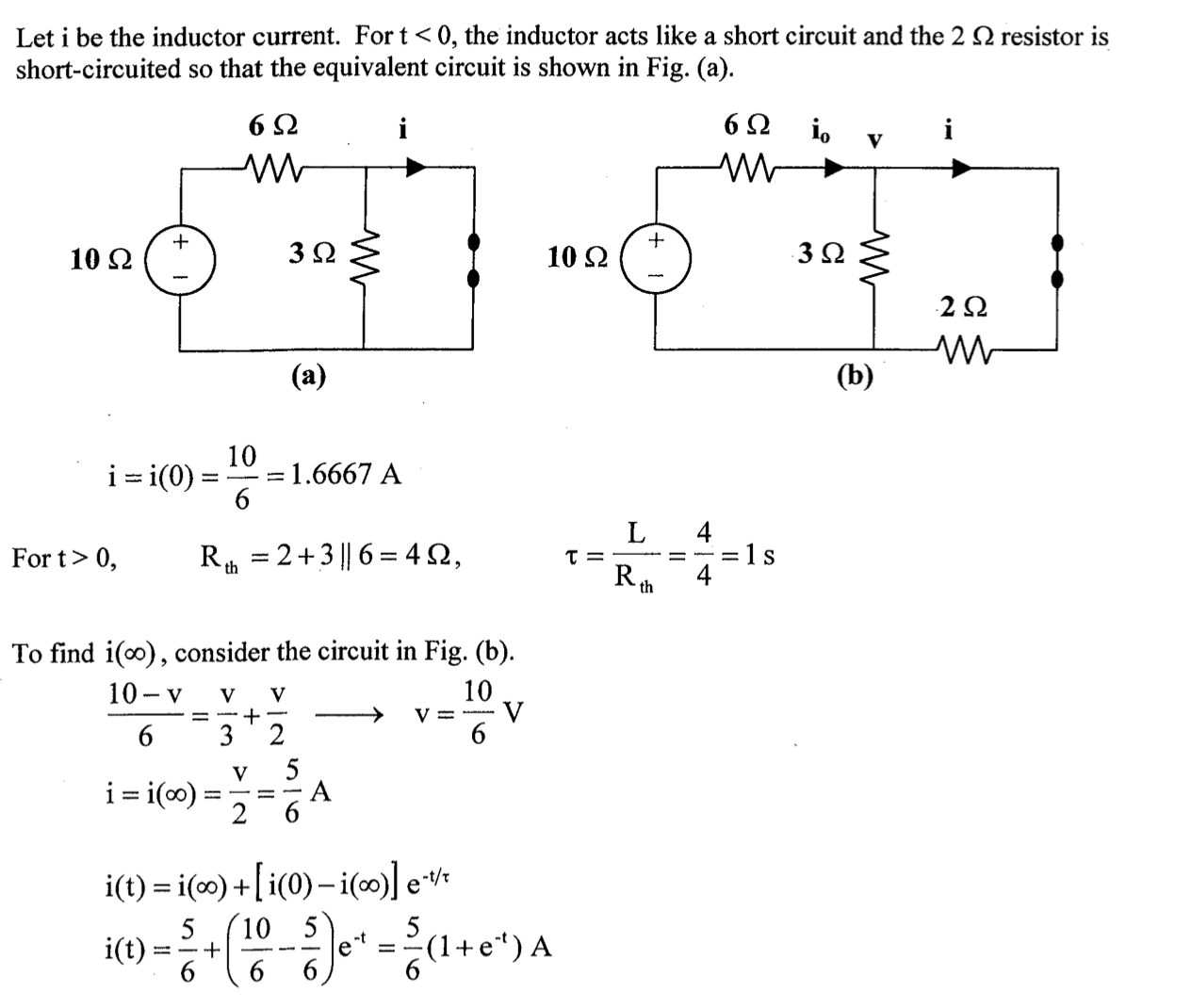
  4. 解：

    对左侧电路进行戴维南等效，化简电路图如下所示：

    image-20220906084437139

该电路的单位阶跃响应为

由齐次性和叠加性得实际响应为：

另外，也可以分段表示结果：

  1. C。 和时间常数不变， 加倍，写成三要素表示形式，可获得结果

  2. 解：

  3. 解：

    开关在 1 位置时， 。

    时刻之后，将电感以外电路进行戴维南等效，求得：

    时间常数为

    边界条件为

    应用三要素法，得到：

    ​

    ​

  4. 解：

    由题意可知，其为零状态响应，。

    ​

    ​

    外施电源法（端口电压 ，端口电流 ）求等效电阻：

    ​

    ​

    因此，

  7. 解：

    开关在位置 A 时，可解得：

    ​

    时转换到位置 B 后，从电容两端看进去的等效电阻为

    ​

    ​

    电路稳定后，有

    因此，可得：

    ​

  8. 解：

    初始条件

    边界条件

    对除了电感外的部分电路外施加电压 求等效电阻：

    ​

    不妨取 ，得：

    ​

    ​

    因此，

    ​

  9. 解：

    (1) 0 < t < 2 s 时

    ​

    ​

    ​

    ​ ，0 < t < 2

    代入边界条件，解得：

    ​

    (2) t ≥ 2 s 时

    ​

    ​

    ​

    ​

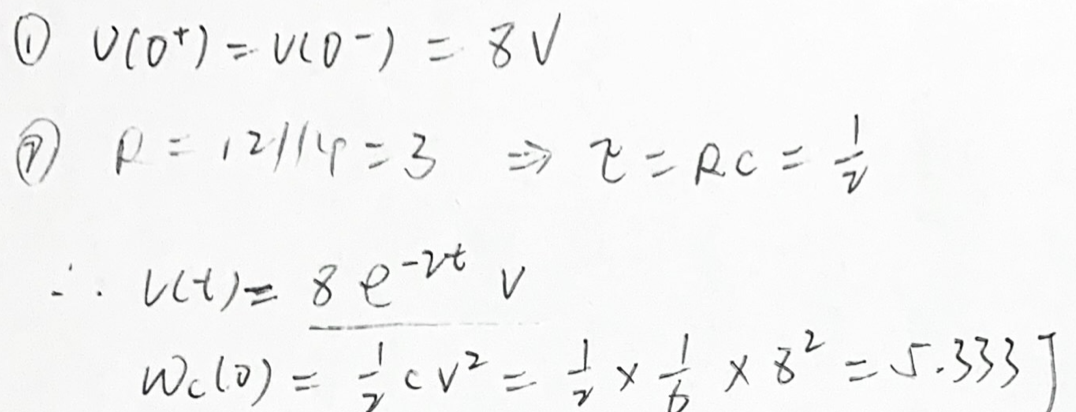
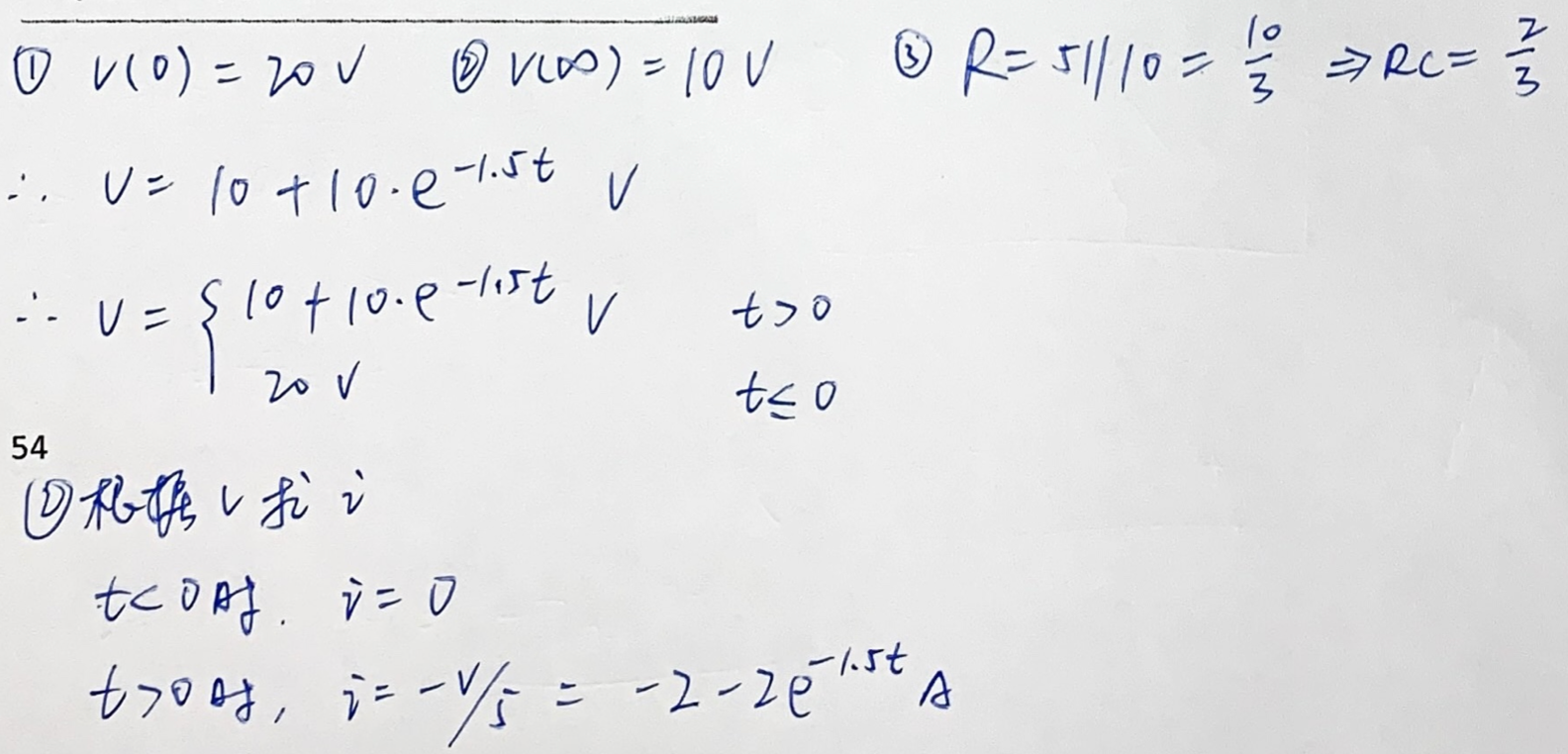
  10. ima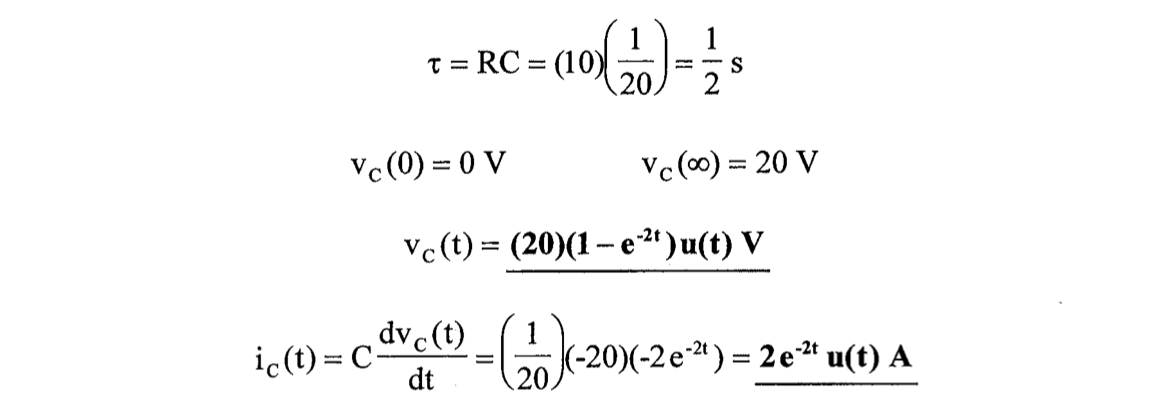ge-20221014155952427
  11. image-20221014160429061
  12. image-20221014160706569

  13. A

  14. image-20221016173417320
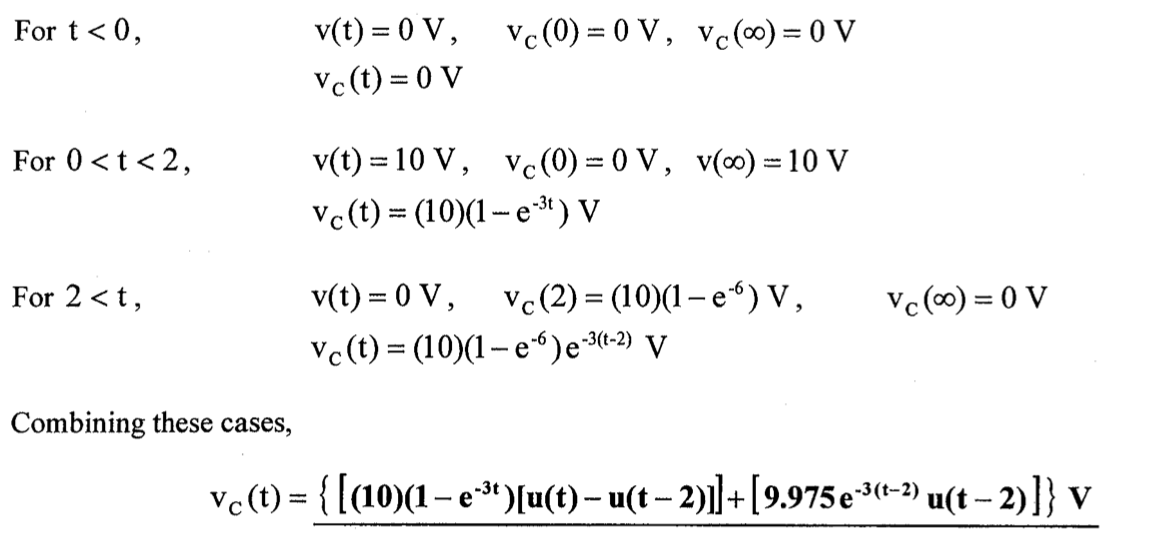
  15. image-20221016173645552image-20221016173707312
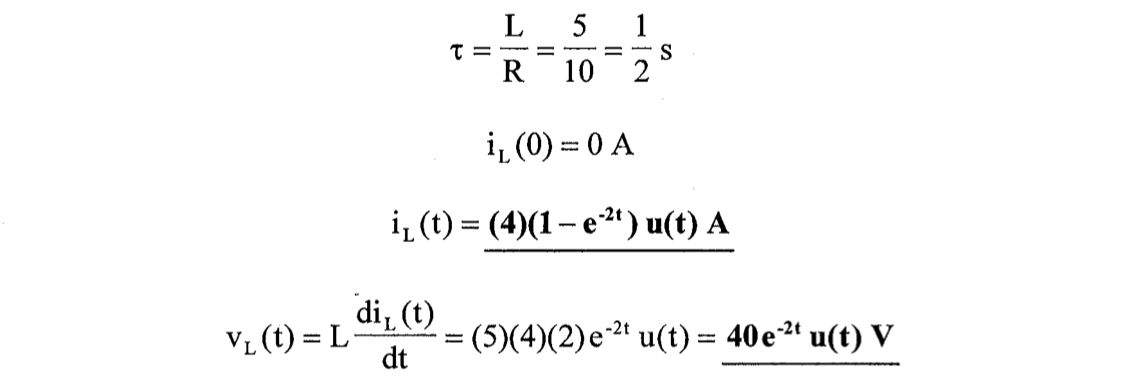
  16. image-20221016173904315
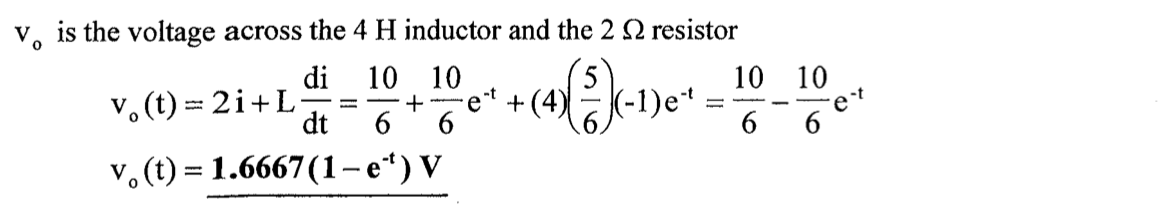
  17. image-20221016174107032image-20221016174122675

知识点2：二阶电路的响应 ​

1、如下图所示电路，开关已长时间处于A位置，t = 0 时刻转向B位置。求 t＞0 时的 和 。

4-2-1

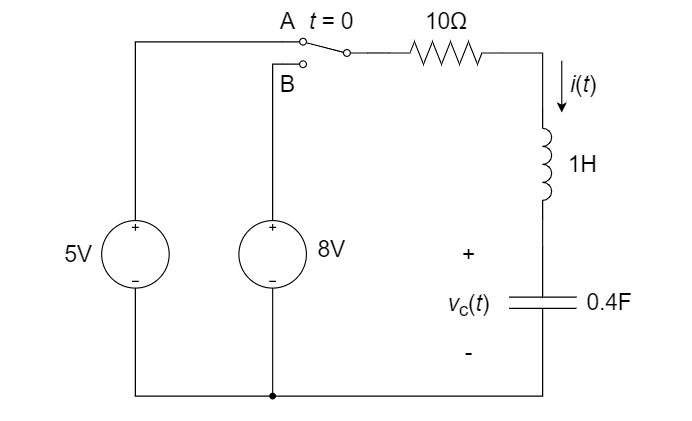
2、如图所示电路中，已知 = 5 Ω， = 1 Ω，L = 1 H，C = 0.25 F，V = 24 V。t = 0时开关断开。求 t > 0 时的 和 。

4-2-3

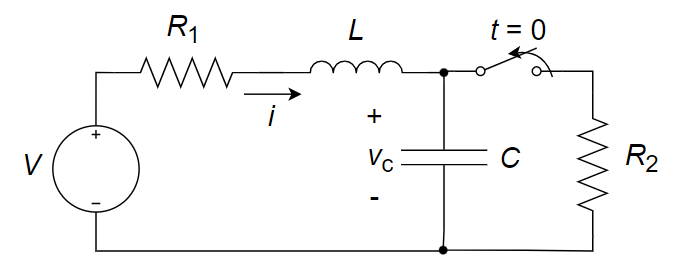
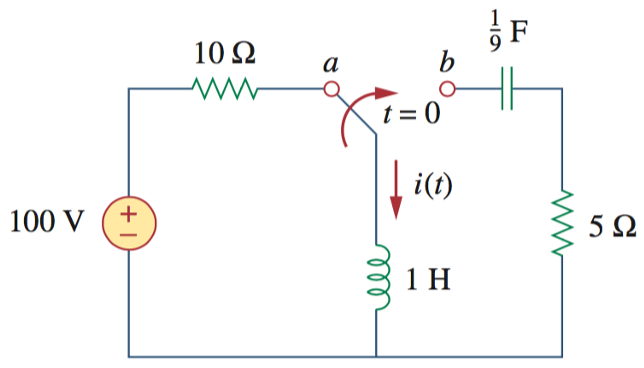
3、如图所示电路，开关置于 a 已经很久，在 t = 0 时开关打至b，求电流 。

4-2-4

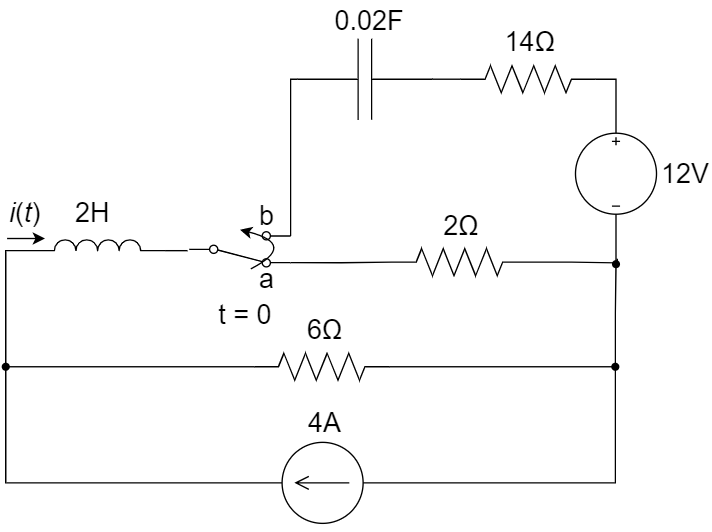
4、如下图所示电路，开关闭合时电路处于稳态，在 t = 0 时开关打开，求 t > 0 时的 。

4-2-5

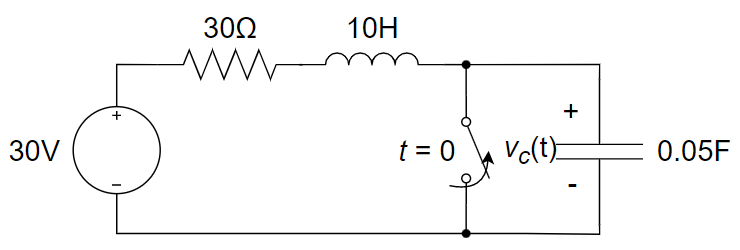
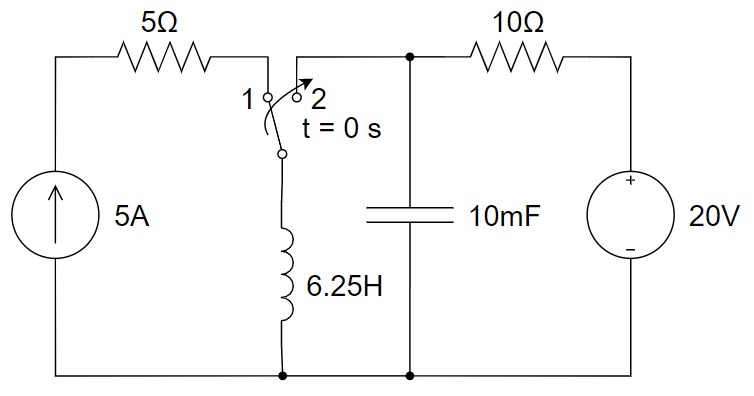
5、如下图所示电路，在 t = 0 时刻前，开关在位置 1 时电路已达到稳定状态，t = 0 时开关由位置 1 合向位置 2 ，求 t > 0 时，流过电感的电流。

4-2-6

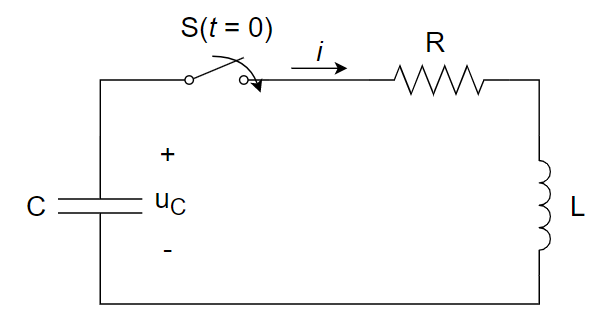
6、下图所示电路中，电容原先已经充电， 。试求：

(1) 开关闭合后的 和

(2) 见第5章-知识点1-第12题

4-2-7

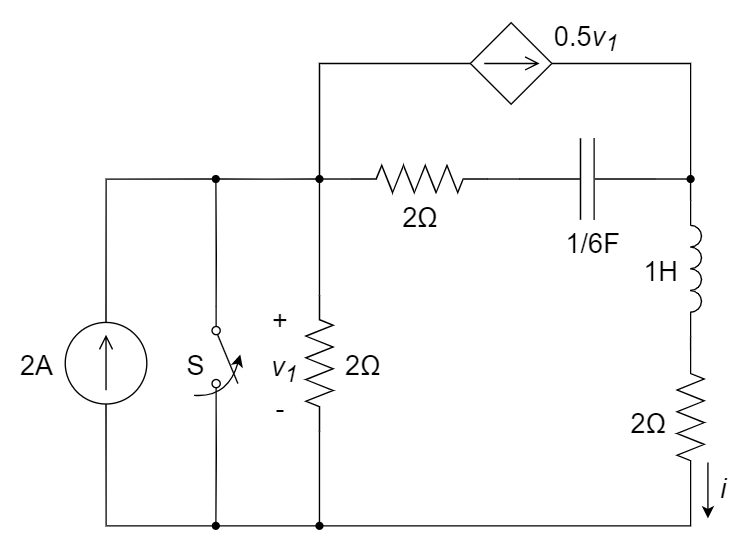
7、如下图所示电路，当 t = 0 时刻打开开关，求电流 的响应。

4-2-8

8、下图中，开关在 时刻从 切换到 ，求 时刻的

image-20221014162506324

9、下图中，求 时刻的

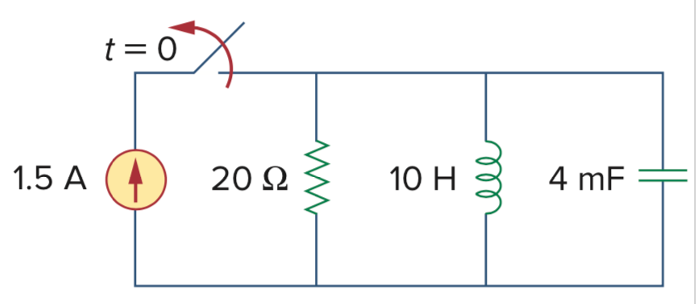
image-20221014162703560

10、下图中，求 时刻的 和

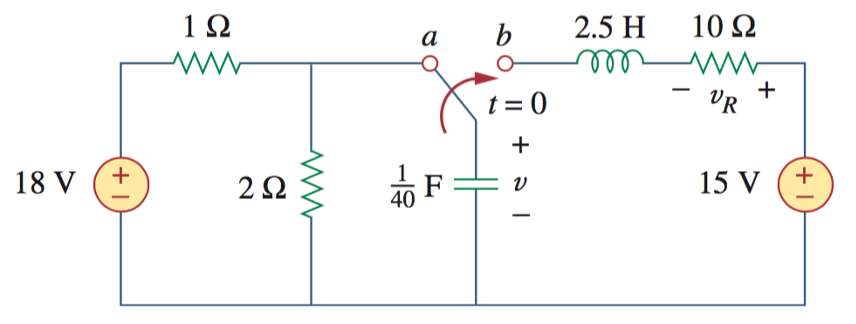
image-20221014162946042

11、下图中，求 时刻的 和

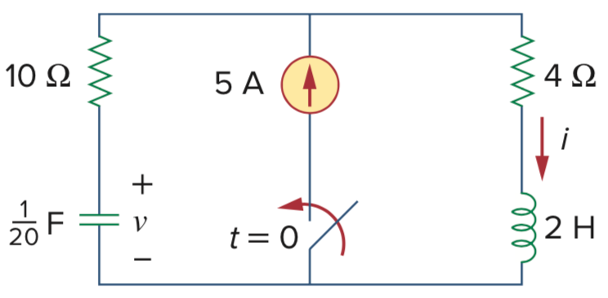
image-20221014163147176

12、如下图所示电路，电容初始储能为0，在 时开关 S1 开路， 时刻，开关 S2 转接到另一端，求 和 时电容两端电压 。

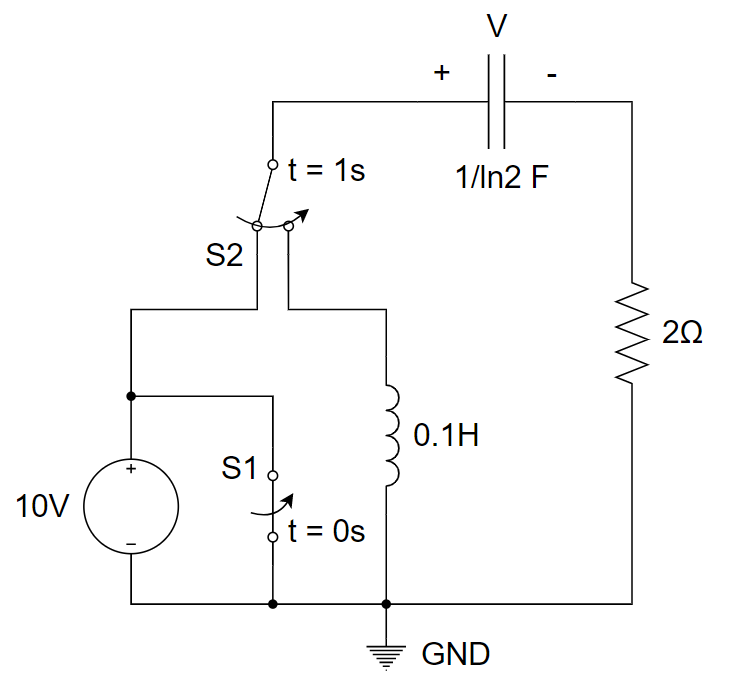
image-20221108130953018

参考解答

  1. image-20220906093928168

  2. image-20220906121204112image-20220906121452879

  3. 解：

(1)在 时，

(2)当 时，可以将 RLC 电路简化如下：

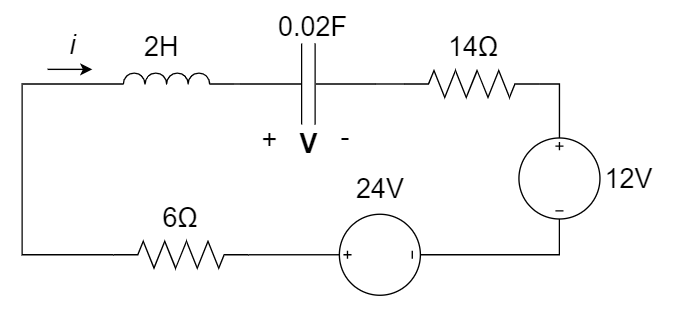
image-20220906121809122

因为 ，所以为临界阻尼响应。故有：

  1. 解：

(1) ，

​

​

(2) 求解 natural response

解-4-2-5

​

​

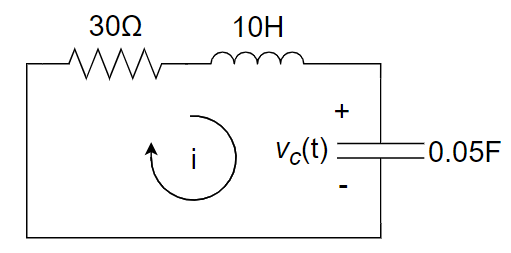
​ 将(1)中的边界条件代入上式，得到：

​

  1. 解：

    根据诺顿等效转换为二阶并联RLC电路，。

    列出方程

    可得：

    初始条件，

    ​

    ​

    解得：

  2. 解：

    ​

    代入R、L、C值，计算得到特征根

    ​

    初始条件

    ​

    ​

    代入初始条件，求解得到

    ​

    ​

  3. 解：

    电流 的响应方程为：

    ​

    ​

    ​

    特征根为：

    ​

    由稳态模型有：

    ​

    ​

    ​

    将边界条件

    ​

    ​

    其中，

    代入得到：

    ​

    故而

  4. image-20221014162540938
  5. image-20221014162732111
  6. image-20221014163023557
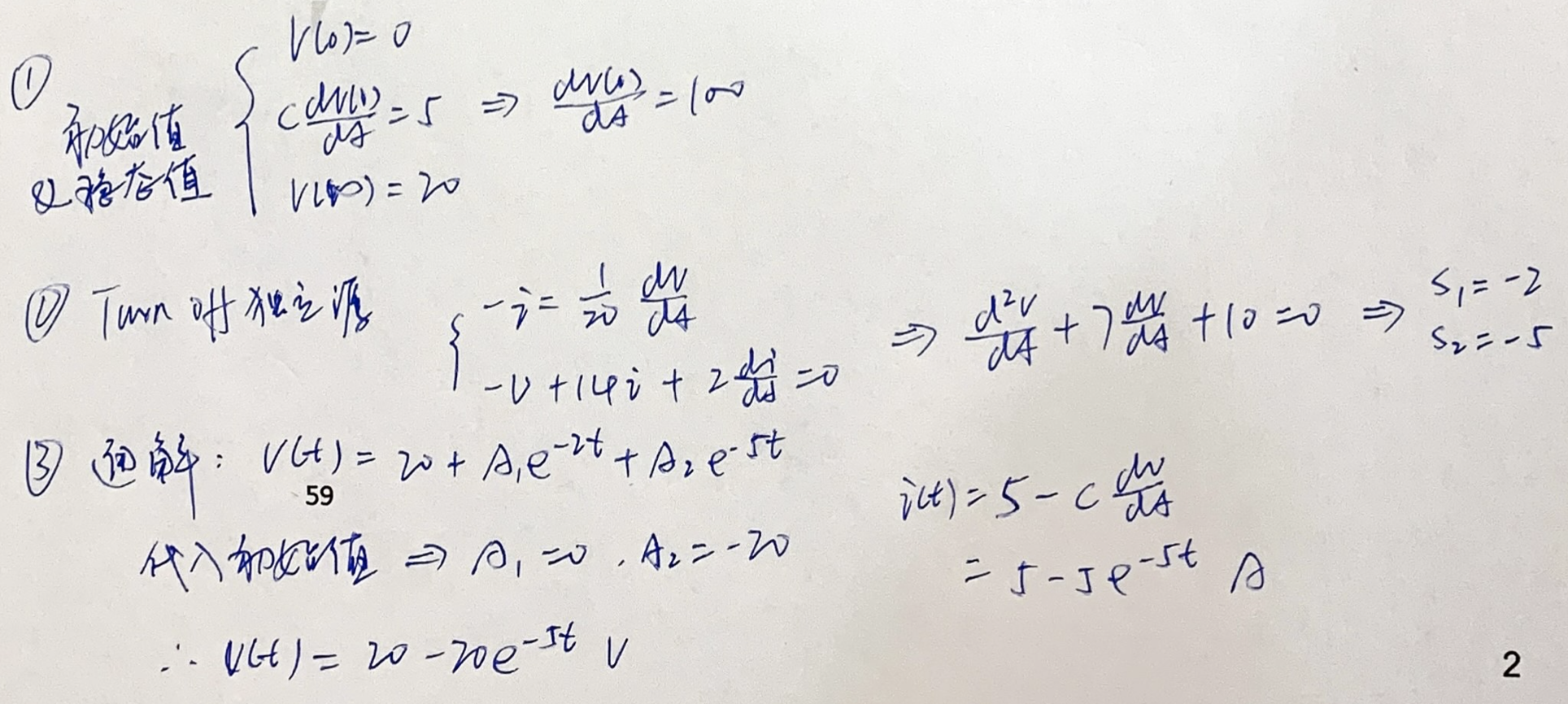
  7. image-20221014163210595

  8. 解：

    (1) 时

    ​

    ​

    ​ ，，

    ​

    ​

    (2)

    ​

    ​

    ​ ，

    ​

    ​

    ​

    ​

    ​ ，

    ​ ，

    ​

    ​

知识点3：阶跃响应与冲激响应 ​

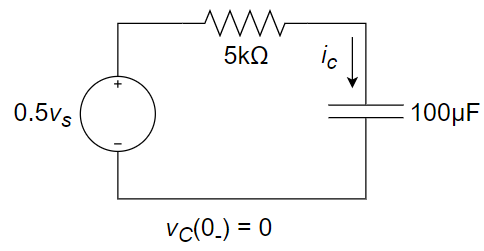
1、如下图所示电路，已知两个电容的初始电压均为 0，求 t > 0 时 vo 的表达式，其中 u(t) 为单位阶跃函数。

4-3-1

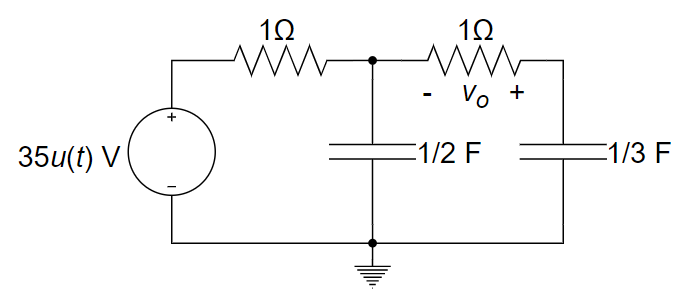
参考解答

  1. 解：

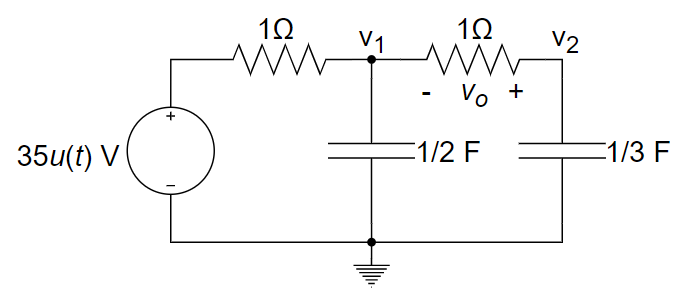
    image-20220906141502284

    ​ turn off 电压源，求齐次方程的通解

    ​ 将 代入 (1) 式中，得：

    ​ 将 代入上式，得到：

    ​ 流过 的电流

    ​ 故

知识点4：其他 ​

1、换路是指电路的结构与参数突然改变，或激励的突然变化。换路时，电路服从的规则称为换路定则。换路定则1：如果流经电容的电流 为有限值，那么电容上的 ________ 在换路瞬间不会突变。换路定则2：当电感电压 为有限值时，电感中 ________ 在换路瞬间不会突变。

2、电路时域全响应可分解为零输入响应与零状态响应的组合，零输入响应是指当电路没有 ________ 信号时的激励响应；零状态响应是指电路无 ________ 时，电路的响应仅由外加信号的激励响应。

参考解答

  1. 电压 电流
  2. 外加 初始储能