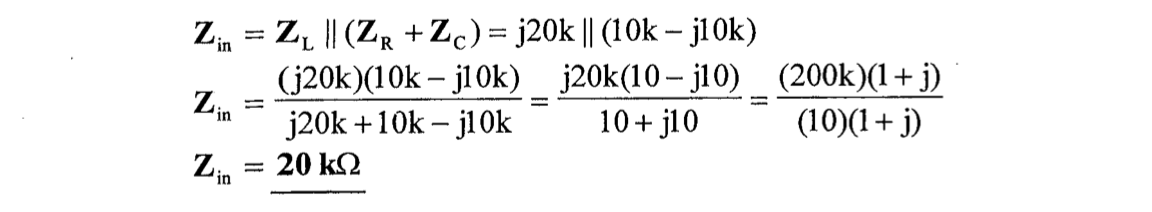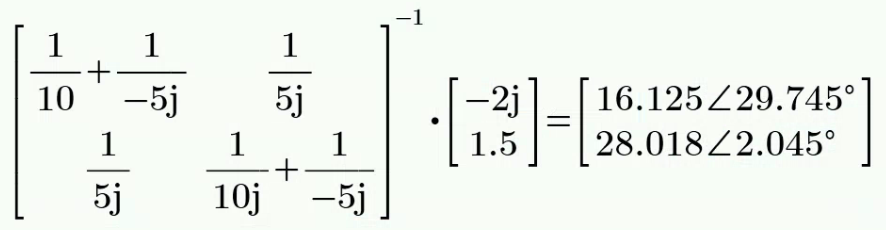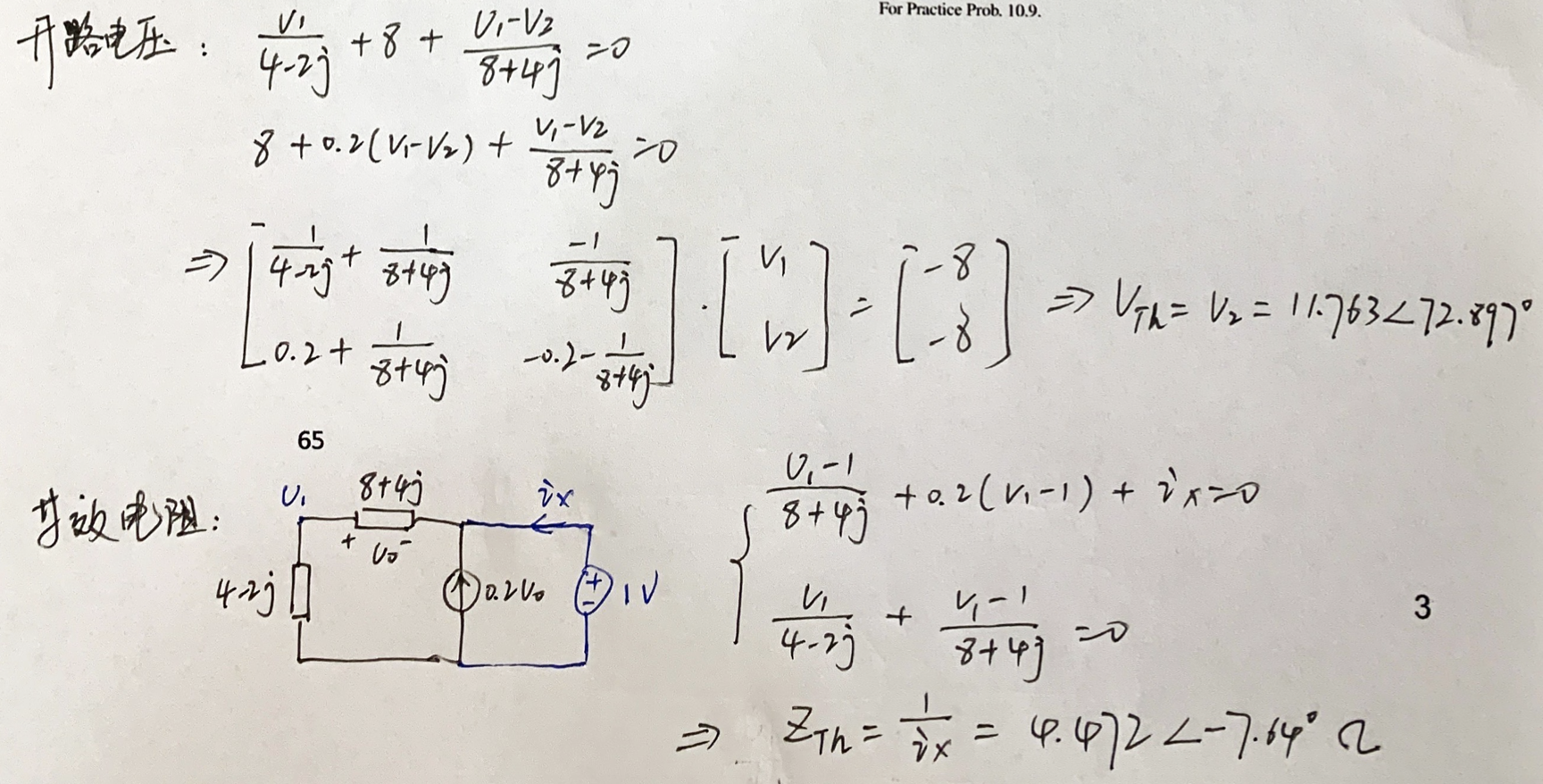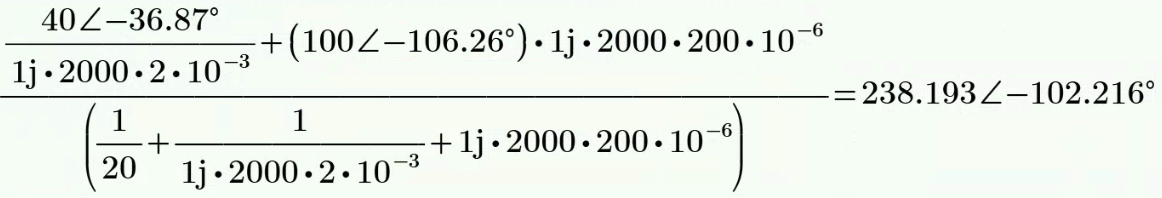正弦稳态电路的相量分析

INFO

5. 正弦稳态电路的相量分析（建议2学时）

5.1 正弦量的基本概念

​ 5.1.1 正弦量的重要特性参数

​ 5.1.2 正弦量的相量表示

5.2 正弦稳态电路的相量分析方法

​ 5.2.1 电路基本物理量的相量描述

​ 5.2.2 基尔霍夫定律的相量形式

​ 5.2.3 电路定理在相量域的推广（包括叠加定理、戴维南定理和诺顿定理）

​ 5.2.4 电路分析方法在相量域的推广（包括网孔电流法和节点电压法）

TIP

1. 三角函数图示记忆方法

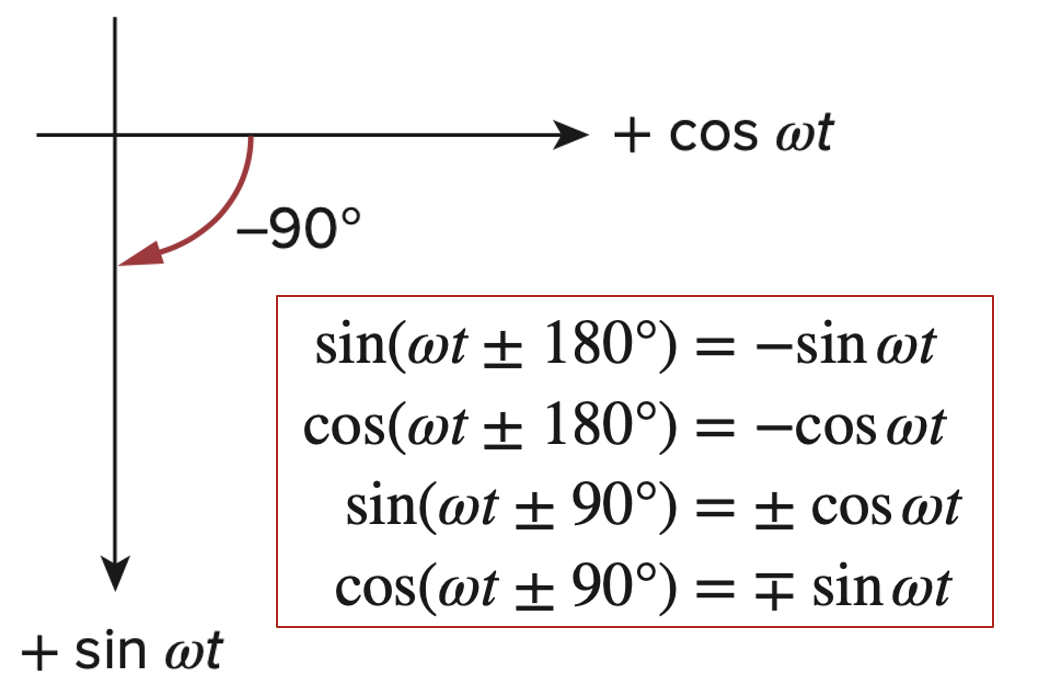
2. 正弦交流电量的概念与特性参数

   • • , 幅值（amplitude），或振幅

     • , 角频率（angular frequency）

     • , 相位（phase），或“初始相位”

     • , 幅角（argument），或“相位”

     • 正弦函数的三要素：幅值、角频率、初始相位

   • 瞬时电压超前（leads） 瞬时电压 相位

   • 有效值：一个时变周期电压在一个周期内消耗在电阻上的功率，可以用一个恒定的电压来等效，该恒定电压就是该时变电压的有效值。当时变电压为正弦函数时，有效值为其峰值的

3. 相量形式与相量图

   • 相量（phasor）是由正弦信号的振幅（）和相位（）构成的一个复数

     

   • 时域 to 相量域（频域），好处是少了时间量，代价是需要复数运算

     • 时域 to 相量域：pick up 振幅和相位，构成一个复数，隐含频率信息 ()

     • 相量域 to 时域：乘以 取实部，

     • 在相量域更容易处理积分和微分

       

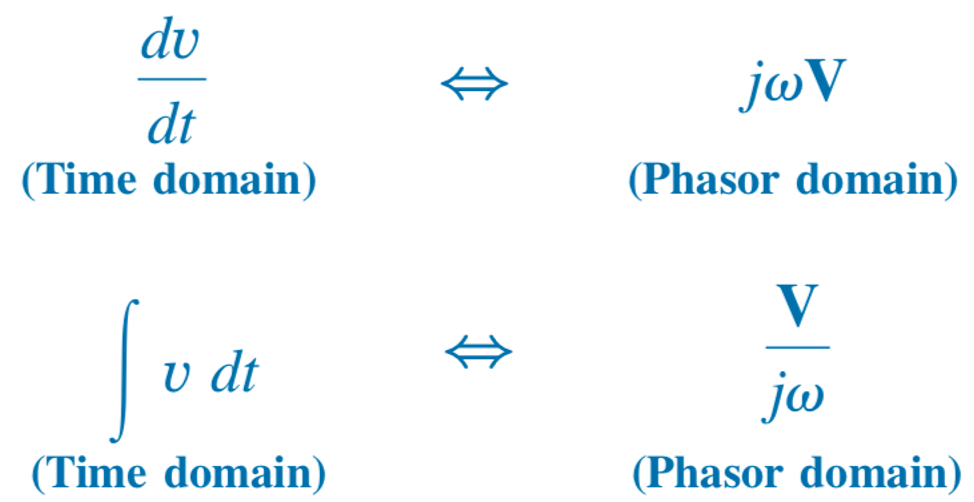
   • 电路分析中，时域量常用余弦形式表示，但正弦形式也是可以的

   • 相量分析法：

     • step 1: 电源、RLC元件等相关电路参量转换到相量域；
     
     • step 2: 在相量域进行电路分析；
     • step 3: 将结果从相量域转换到时域；
     • tips: 如果初始电路含有不同的 ，则需对不同 单独分析，在时域上叠加；

   • 阻抗和导纳：电阻和电导在频域中的推广

     • ；（阻抗），（电阻），（电抗） ；
     • ，（导纳），（电导），（电纳）；

   • 相量图即复平面图

     • 因为较多情况是“施加电压，求电流”，所以在描述相位关系时，常用“电流超前/滞后电压多少相位”的形式

     • 感性电路，电流滞后电压

     • 容性电路，电流超前电压

       

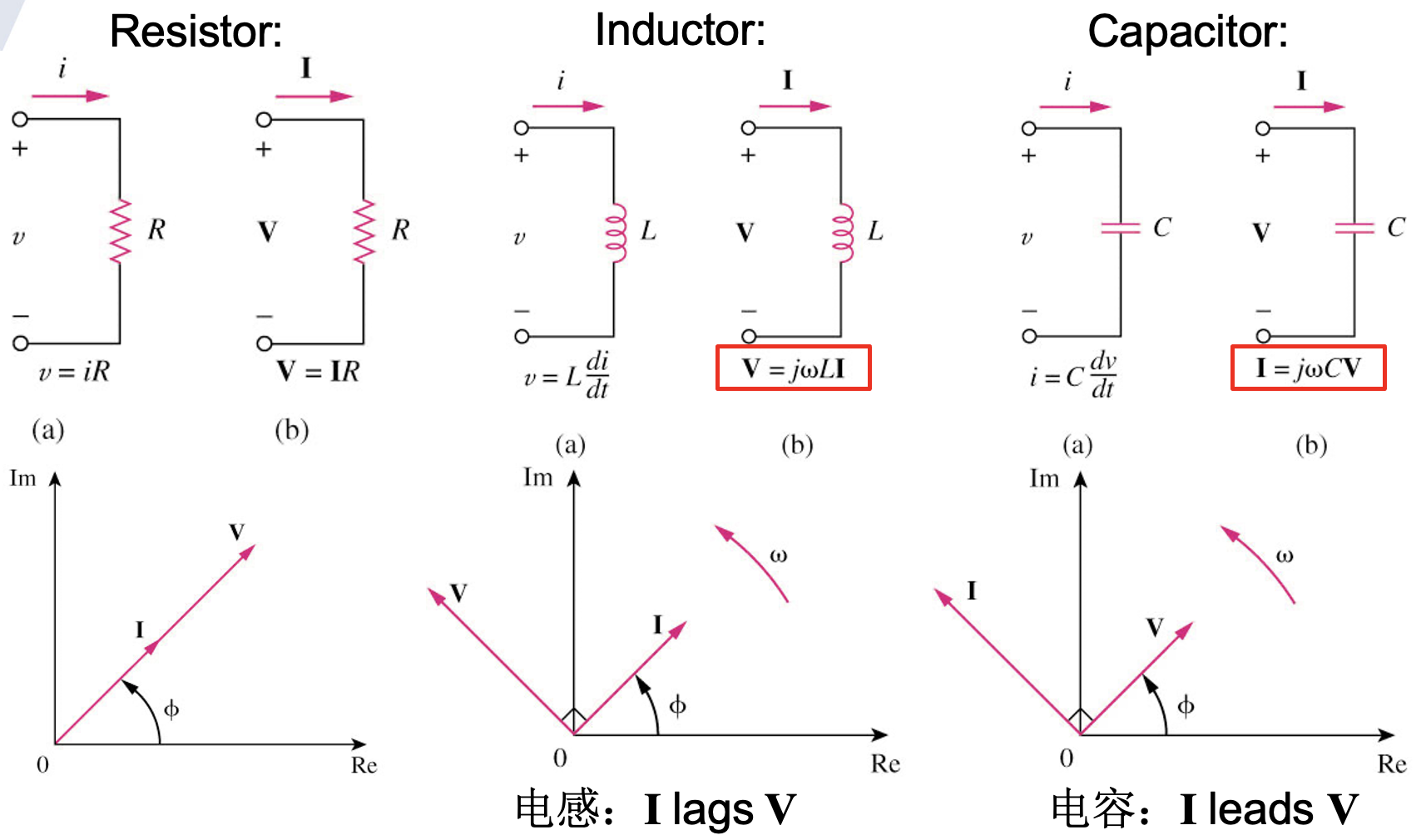
4. 频域（相量域）的相关电路定理：

   • 时域中的电路定理在相量域中同样适用
   • 叠加定理需注意：电路中若有不同的频率，只能时域叠加，不能相量域叠加

习题及参考解答

知识点1：正弦交流量的概念与特性参数

CH04-KP1-01: 有效值为 1V 的正弦交流电压信号衰减 3dB 之后的信号最大值是 ________ V。

A.

B.

C.1

D.

参考答案	C

解析：

对于正弦波，有效值为峰值的 ; 3dB 表示半功率，也即电压幅度为峰值

CH05-KP1-02: 正弦交流激励下，电容两端的电压 ________ 通过它的电流 ________ 度。

A. 超前

B. 滞后

C. 45

D. 90

E. 180

参考答案	B，D

解析：

根据电容电压电流的频域约束关系,

CH05-KP1-03: 正弦交流激励下，电感两端的电压 ________ 通过它的电流 ________ 度。

A. 超前

B. 滞后

C. 45

D. 90

E. 180

参考答案	A，D

解析：

根据电感电压电流的频域约束关系,

CH05-KP1-04: 电流 和 相位差是 ________ ，其中相位超前的是 ________ 。

参考答案	，

解析：

将 转换成 形式，；

CH05-KP1-05: 正弦电压 对应的相量表示为 ________ 。

A.

B.

C.

D.

参考答案	D

解析：

根据定义

CH05-KP1-06: 正弦量的三要素为________ 、________ 和 ________。

参考答案	幅值、角频率、初相位

解析：

根据定义

CH05-KP1-07: 电流 的相位 ________ （超前/滞后） ________ 度。

参考答案	超前，120

解析：

把负号放到cos表达式里面后再比较

CH05-KP1-08: 电压 与电流 相比，相位差为 ________ 。

A. 超前54°

B. 滞后54°

C. 超前36°

D. 滞后36°

参考答案	B

解析：

把 sin 转换为 cos，或把 cos 转换为 sin 后再比较

CH05-KP1-09: 正弦电压向量为 （15是有效值），频率为 50 Hz ，则它对应的瞬时表达式为 ________ 。

A.

B.

C.

D. ​

参考答案	D

解析：

根据定义

CH05-KP1-10: 已知两个支路的电流分别可表示为 ，，比较两者的相位，前者 ________ （超前/滞后）后者 ________ 度。

参考答案	滞后，135

解析：

按惯例，超前或滞后角度的绝对值不超过180°

CH05-KP1-11: 两同频率的正弦电压可表示为 ，，则它们的相位差为 ________ 。

A. 30°

B. 60°

C. 120°

D. 150°

参考答案	B

解析：

化成相同的形式再比较

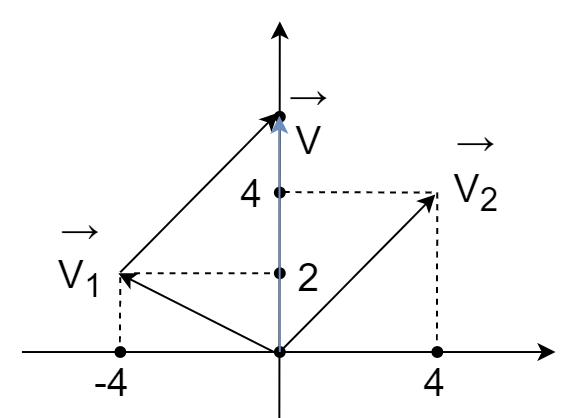
CH05-KP1-12: (1) 根据下图的相量图，求 的相量；

​ (2) 正弦变量 对应的相量为？

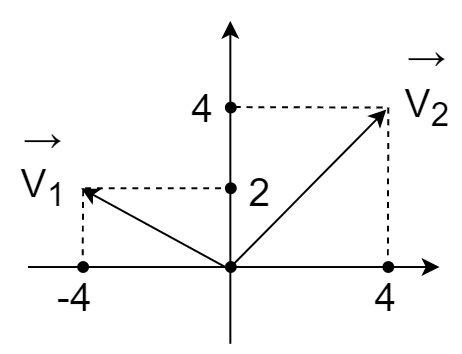
解析：

(1) 方法1：图解法

​ 由图可得：

​ 方法2：

​ 由图可知：，

​ 故而，

(2)

CH05-KP1-13: 正弦交流电路中，以下阐述理解正确的是 ________ 。

A. 如果电路中存在多个不同频率的源，则不能使用叠加定理直接分析电路。

B. 如果通过负载的电流超前其两端的电压，则该负载为感性负载。

C. 如果某无源网络的输入阻抗是，其导纳为 。

D. 电感两端电压超前电流90度，电容两端电压落后电流90度。

参考答案	D

解析：

A, 可以在时域中使用叠加定理，所以错误；B和C显然是错误的。

知识点2：非纯电阻电路的分析

CH05-KP2-01: 以下电桥的平衡条件是 ________ 。

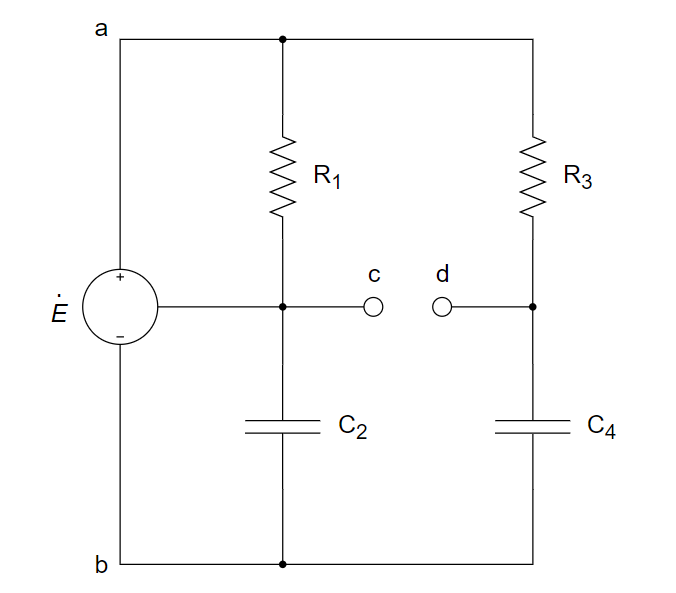
A.

B.

C.

D.无法平衡

参考答案	A

解析：

阻抗按比例

CH05-KP2-02: 若在一个 50 μF 的电容两端施加一电压 ，则流经该电容的电流值为 ________ 。

参考答案	mA 或 mA

解析：

按电容的电压电流约束关系

CH05-KP2-03: 若 RC 串联电路对频率为 100 Hz 的正弦波的阻抗为 (2 - j6) Ω，则该串联电路对频率为 300 Hz 的正弦波的阻抗为 ________ 。

参考答案	(2 - j2) Ω

解析：

根据电容的阻抗定义

CH05-KP2-04: 如果 RL 串联电路对频率为 300Hz 的正弦信号的阻抗为 (1 + j3) Ω，则对频率为 100Hz 的正弦信号，该串联电路的阻抗为 ________ ，构成并联电路时的导纳为 ________ 。

参考答案	(1 + j) Ω ；(1 - j) S

解析：

根据电感的阻抗定义

CH05-KP2-05: 若 RC 串联电路对频率为 100 Hz 的正弦波的阻抗为 (3 - j9) Ω，则该串联电路对频率为 300 Hz 的正弦波的阻抗为 ________ 。

参考答案	(3 - j3) Ω

解析：

根据电容的阻抗定义

CH05-KP2-06: 若 RC 串联电路对频率为 100 Hz 的正弦波的阻抗为 (4 - j16) Ω，则该串联电路对频率为 400 Hz 的正弦波的阻抗为 ________ 。

参考答案	(4 - j4) Ω

解析：

根据电容的阻抗定义

CH05-KP2-07: 右图所示电路中， 。则 = ________ （用极坐标形式表示）

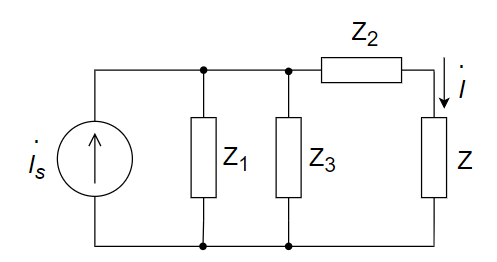
参考答案	1.131∠81.87° A

解析：

可以先并联等效，再按分流计算

CH05-KP2-08: 下图中，若电流 ，电压 ，那么该元件是 ________ 。

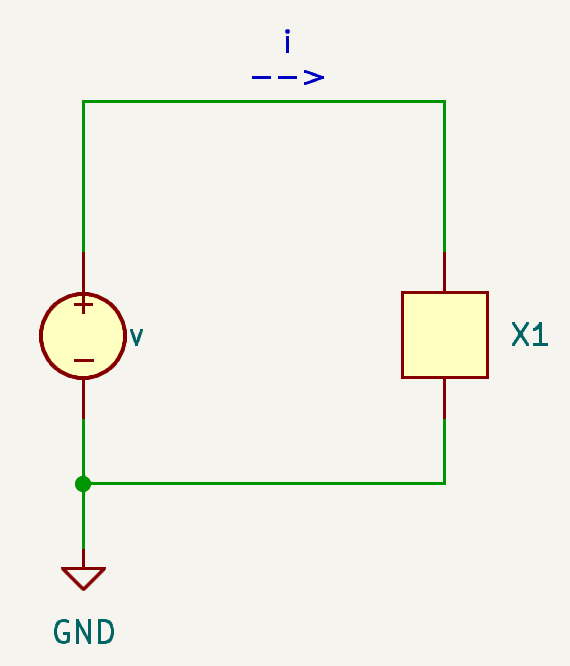
A. 电感

B. 电容

C. 电阻

参考答案	B

解析：

电流与电压的导数成比例，故为电容

CH05-KP2-09: 下图所示电桥的平衡条件是 ________ 。

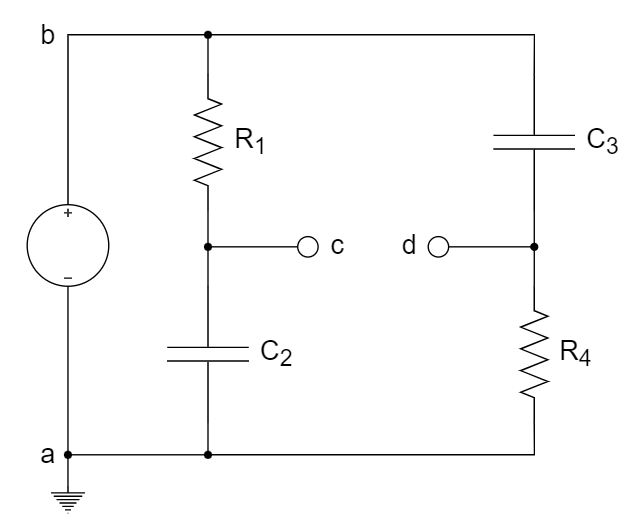
A.

B.

C.

D. 无法平衡

参考答案	D

解析：

无法实现阻抗按比例

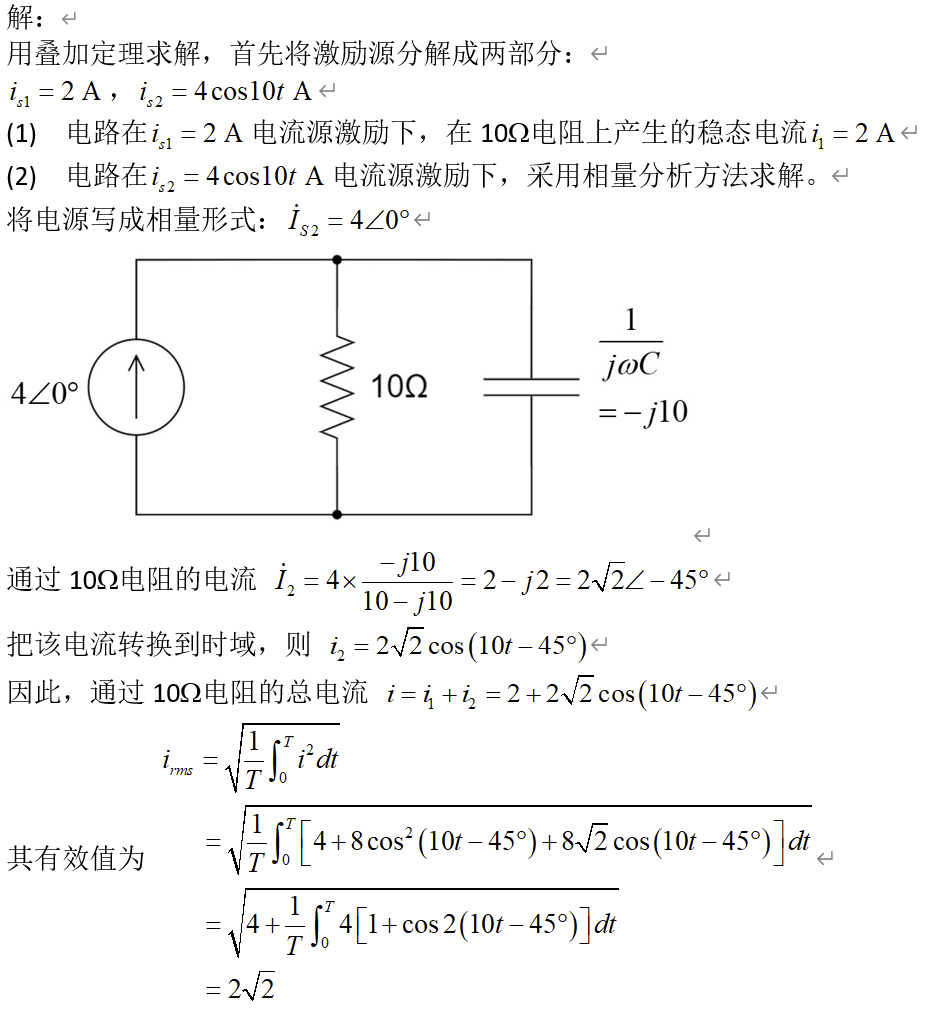
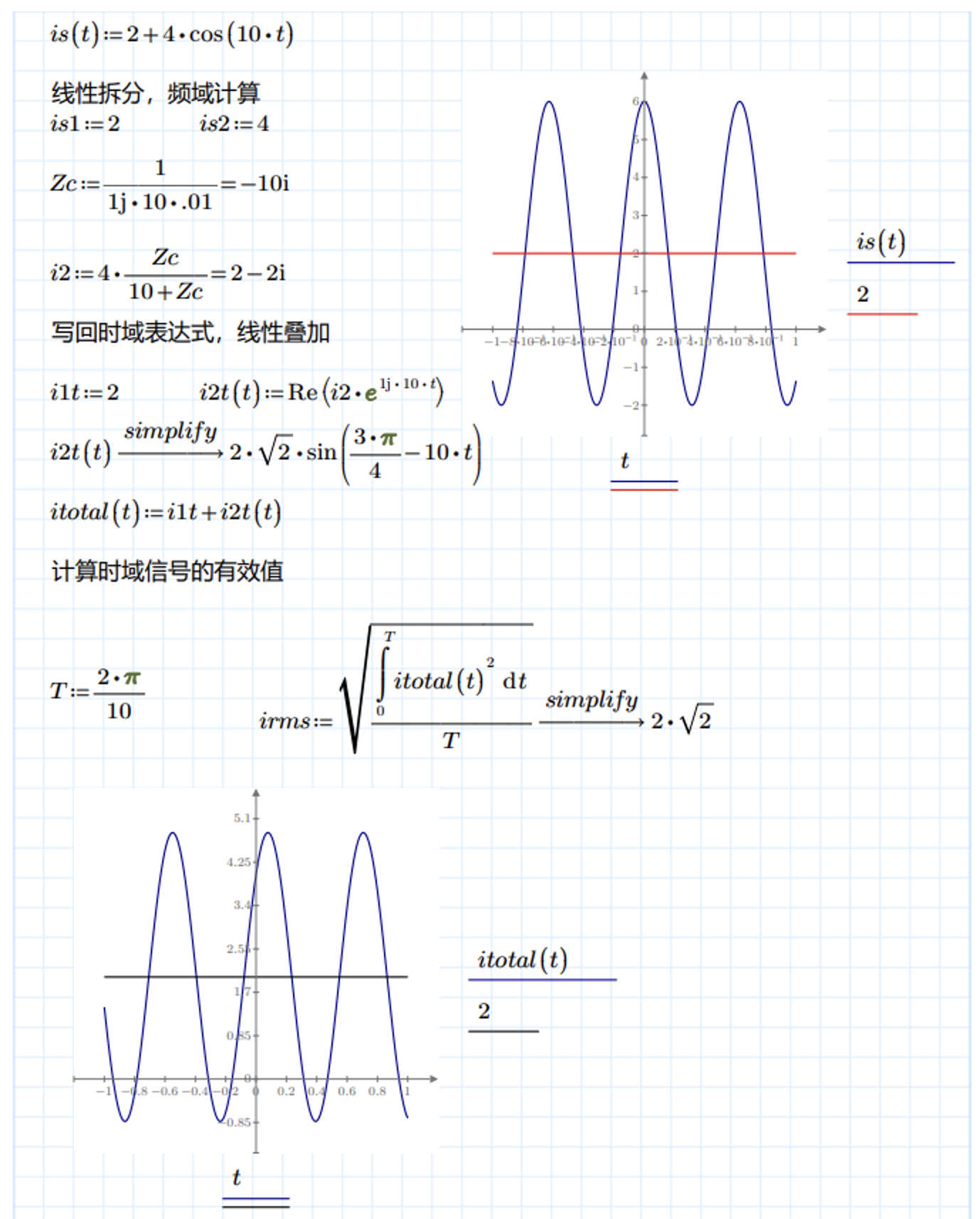
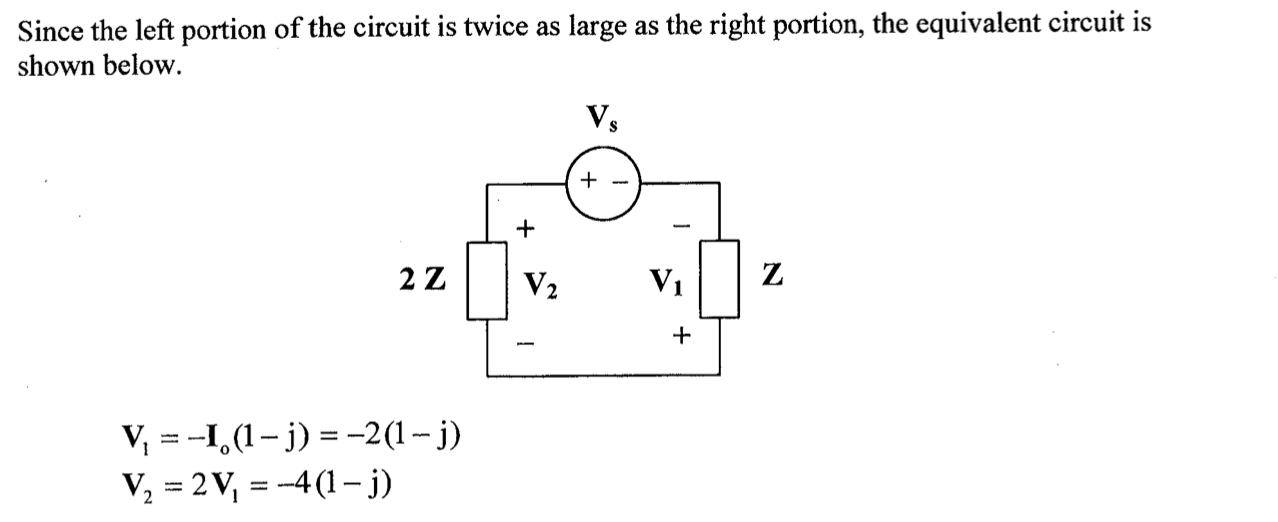
CH05-KP2-10: 下图所示电路中，，通过 电阻电流的有效值应为__ __。

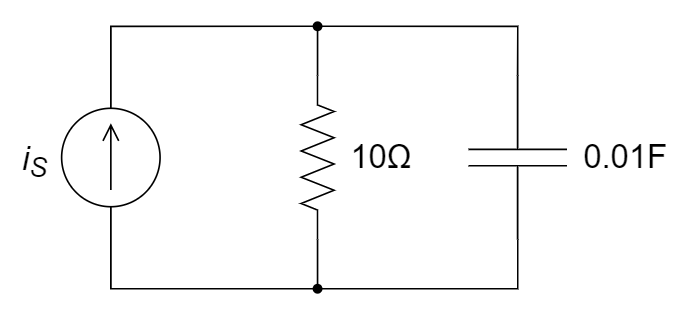
A. 4 A

B.

C.

D. 2 A

参考答案	B

解析：

参考一：

参考二：

CH05-KP2-11: 下图为三个阻抗串联的电路：，，，外加电压 。求电流及各阻抗上的电压。

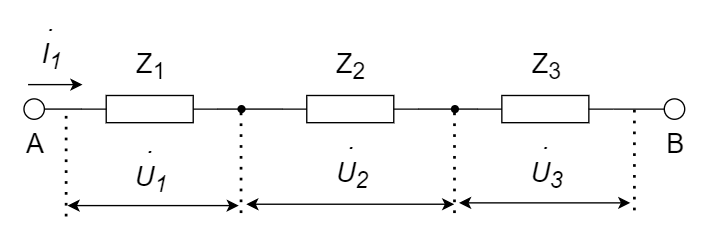
解析：

CH05-KP2-12: 下图中， A，求

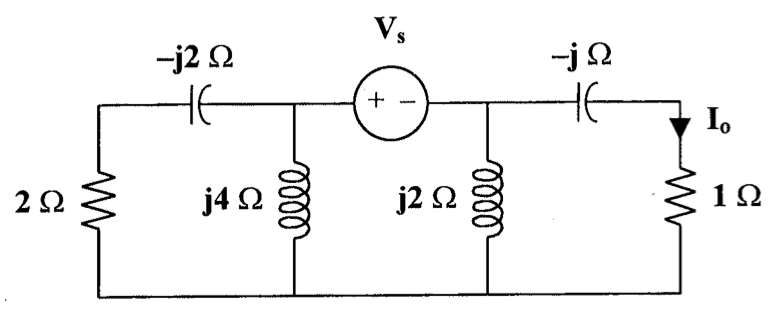
解析：

CH05-KP2-13: 下图中， rad/s，求输入阻抗

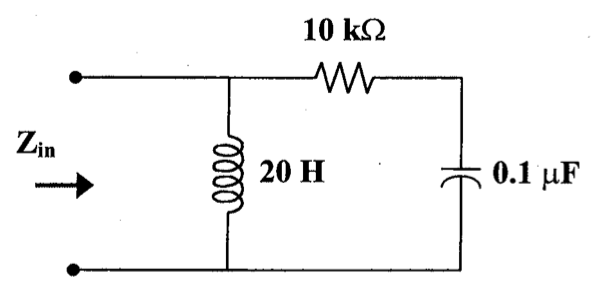
解析：

CH05-KP2-14: 求下图的等效阻抗

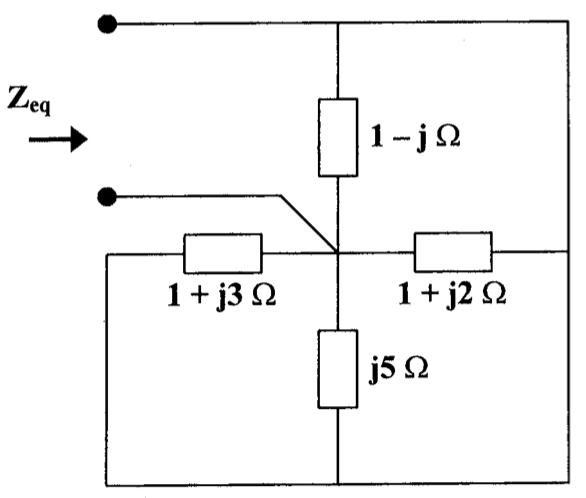
解析：

知识点3：电路定理在相量域的推广

CH05-KP3-01: 用叠加原理求解下图所示电路中的 。

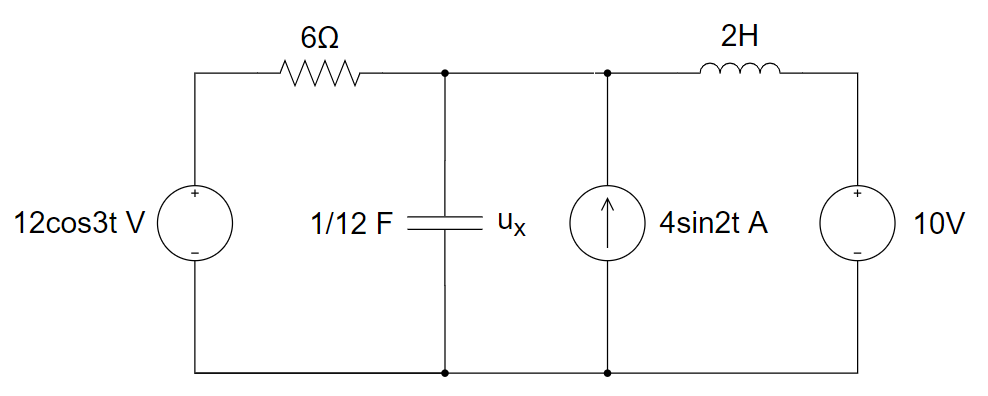
解析：

采用叠加定理，

先考虑电压源 12cos3t V 独立作用时， 电容阻抗为，电感阻抗为

得到 ；

考虑电流源 4sin2t V = 4cos(2t - 90°) V 独立作用时，电容阻抗为，电感阻抗为

得到 ;

考虑电压源 10V 独立作用时：

得到 V;

故 。

CH05-KP3-02: 正弦稳态电路中，系统可以用戴维南定理等效为电源 和等效阻抗 。要使系统传输到负载 上的平均功率最大，负载和系统等效阻抗之间的关系是 ________ 。

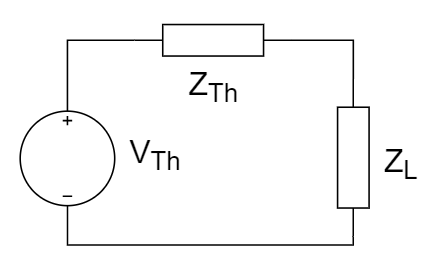
A.

B.

C.

D. ​

参考答案	C

解析：

共轭阻抗匹配

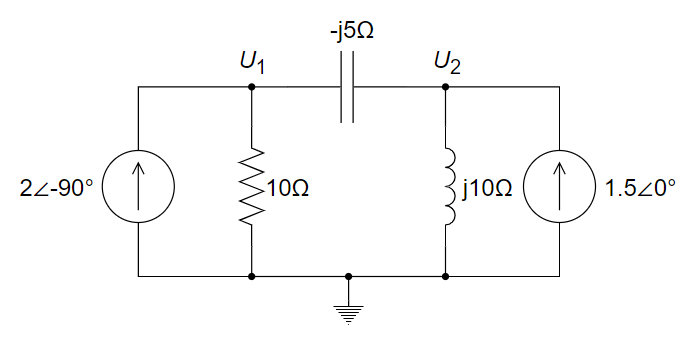
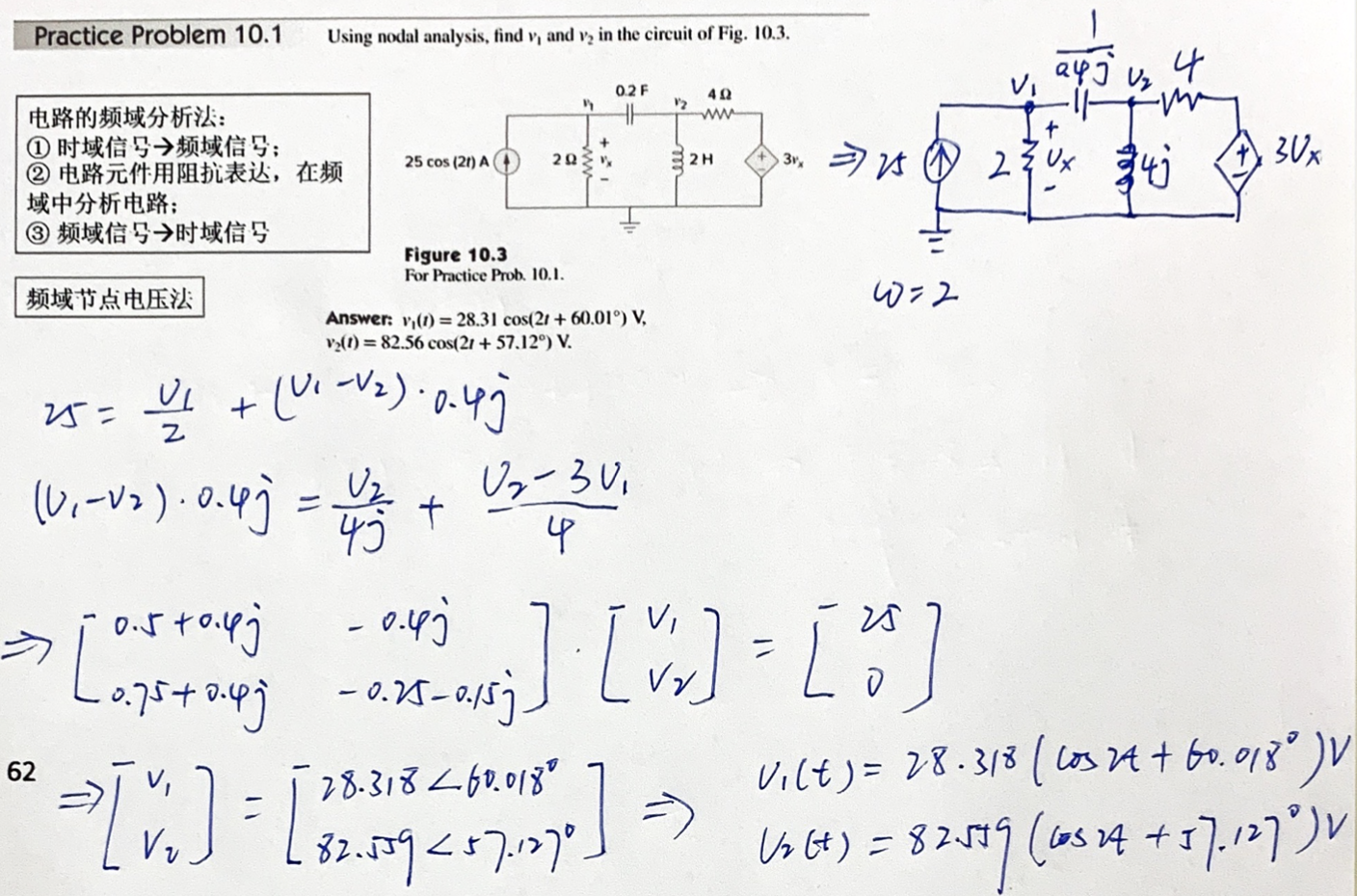
CH05-KP3-03: 用节点电压法求下图所示电路在稳态下的 。

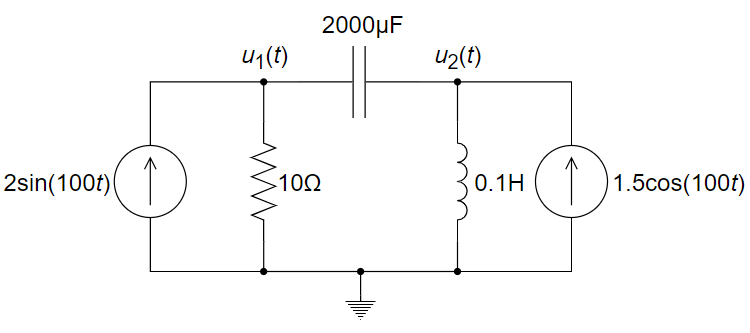
解析：

在频域内求解，给出电路图的相量表示。

对节点 1 和节点 2 分别用 KCL，得到：

将上述两式变成标准形式

对上述方程组求解，得到

转变到时域形式，得到

CH05-KP3-04: 已知下图所示电路中 ， ，求流过电容的电流 。

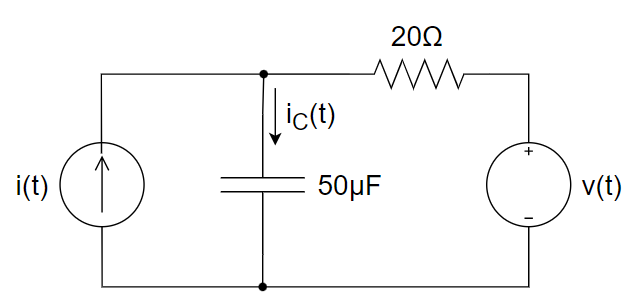
解析：

(1) 仅考虑电流源，turn off 电压源

​

​

(2) 仅考虑电压源，turn off 电流源

​

​

(3) 时域叠加

综上，

CH05-KP3-05: 下图中，ab 左侧部分可用诺顿等效电路等效，求

(1) 诺顿等效电流源 和等效阻抗 ；

(2) 。

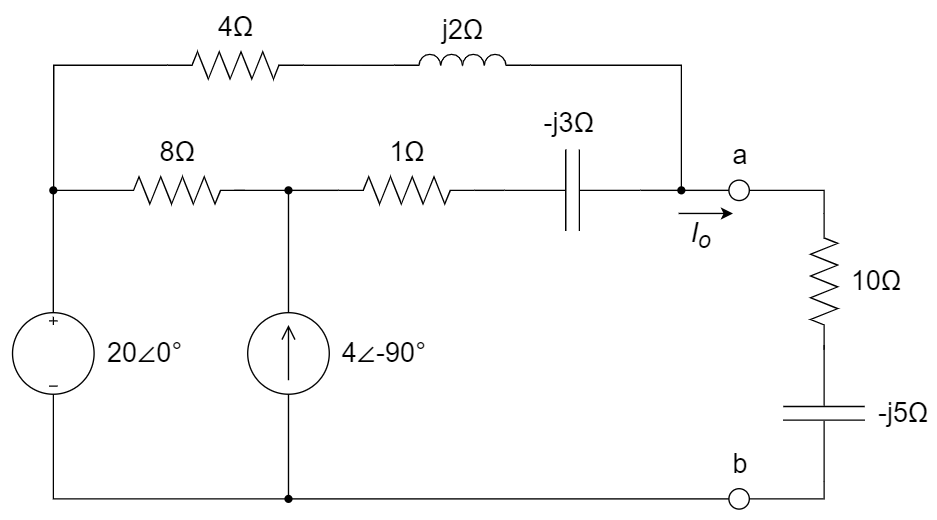
解析：

(1) 输出端短路，求 。

​

(2) 独立源置零，在端口处施加一 1∠0° V 的电压，求等效阻抗 。

​

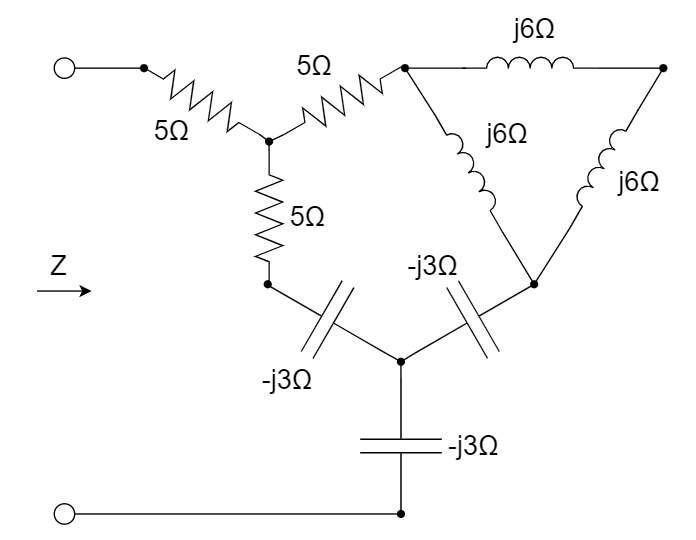
CH05-KP3-06: 计算输出电阻 Z 。

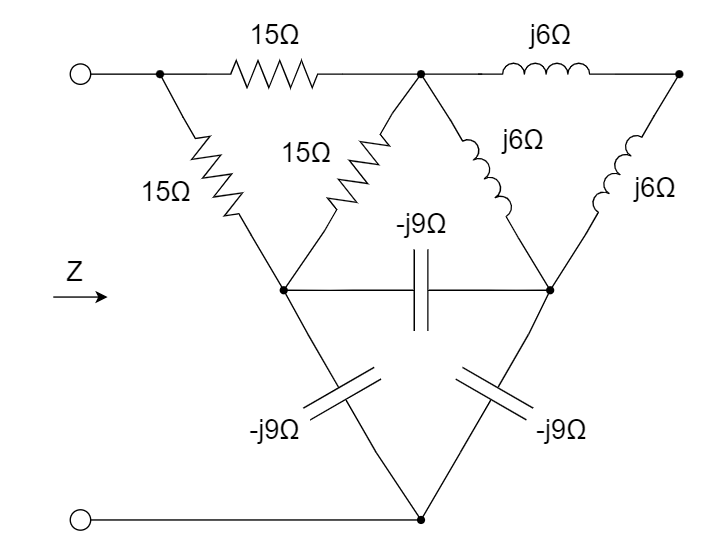
解析：

对左上方小 电阻网络和下方小 电容网络使用 转换，得到：

那么可以得到，电路的等效输出阻抗为

​

​

​

​

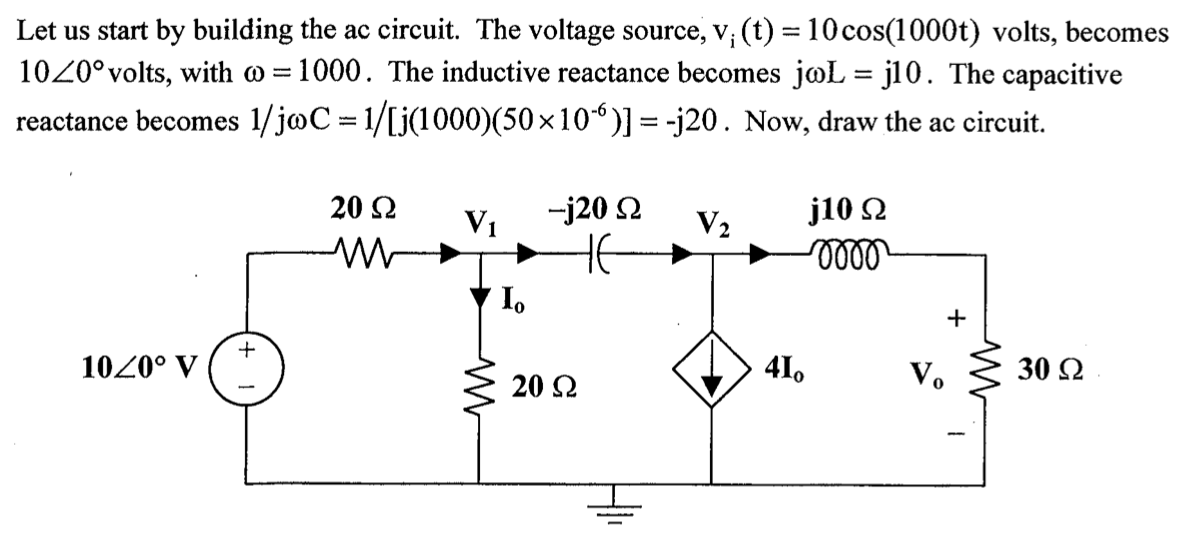
CH05-KP3-07: 请使用节点电压法，分析下面电路，计算 和

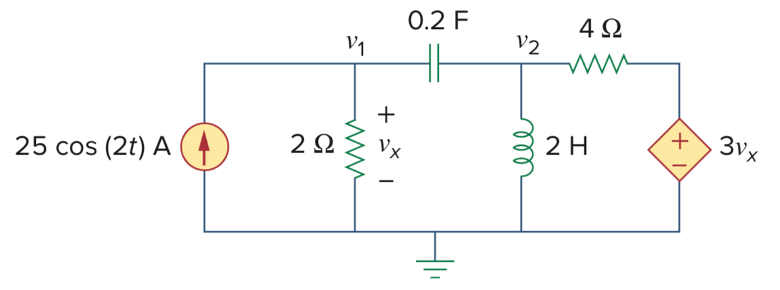
解析：

CH05-KP3-08: 计算下图中的电流

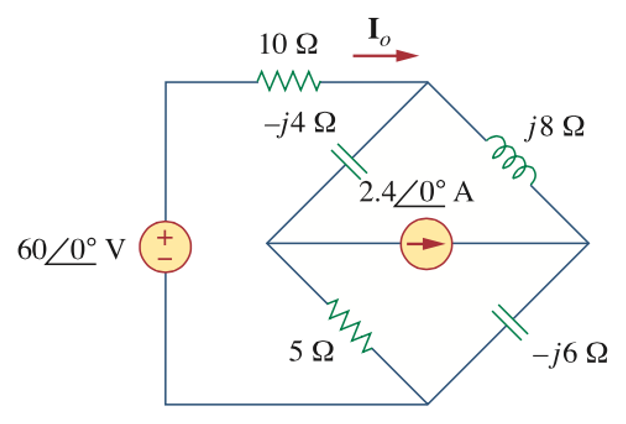
解析：

CH05-KP3-09: 采用叠加定理分析以下电路，计算

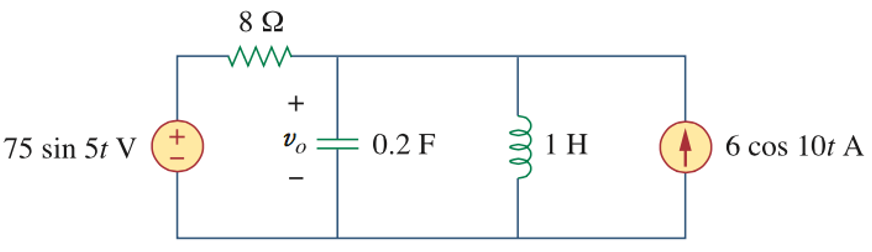
解析：

CH05-KP3-10: 下面电路中，求 端的戴维南等效电路

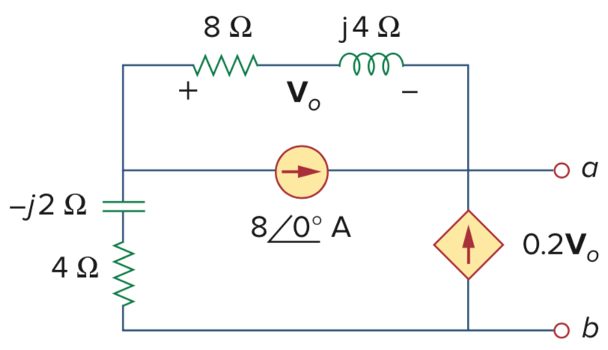
解析：

CH05-KP3-11: 下图中，，请用节点电压法，求

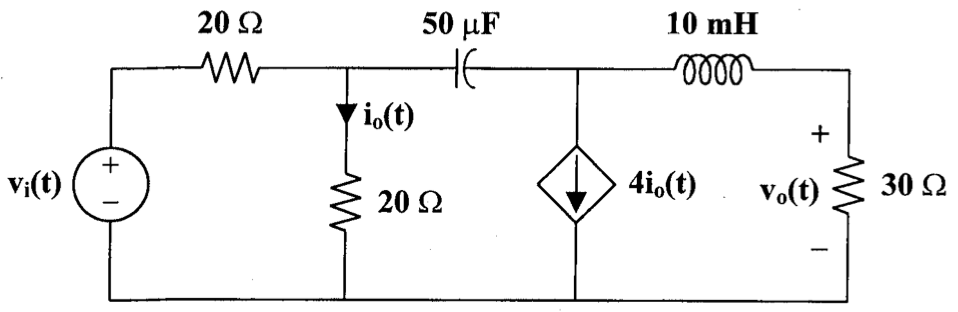
解析：

CH05-KP3-12: 下面电路中， A，请用网孔电流法，求

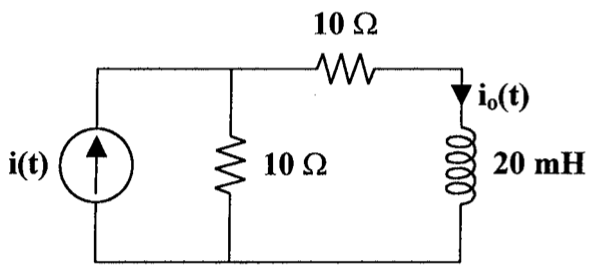
解析：

CH05-KP3-13: 下图中， A，请用网孔电流法，求

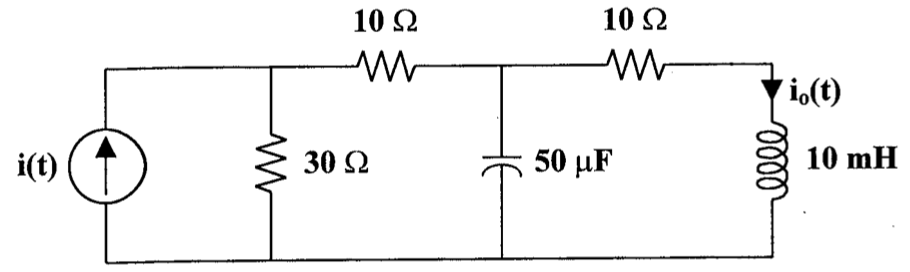
解析：

CH05-KP3-14: 求下列电路的戴维南和诺顿等效电路

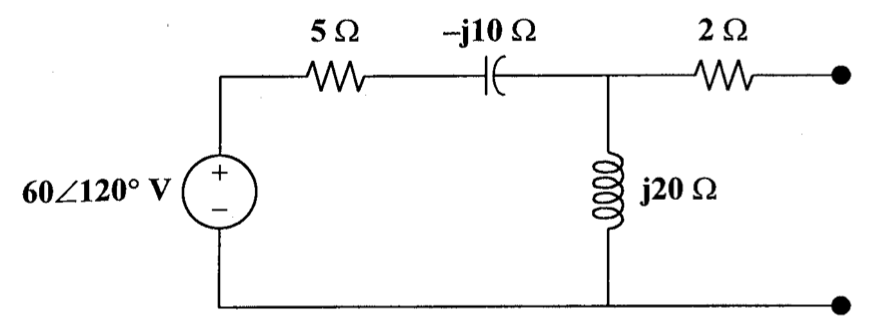
解析：

CH05-KP3-15: 如下图所示电路，已知 ，，用叠加原理求电容两端的电压 。

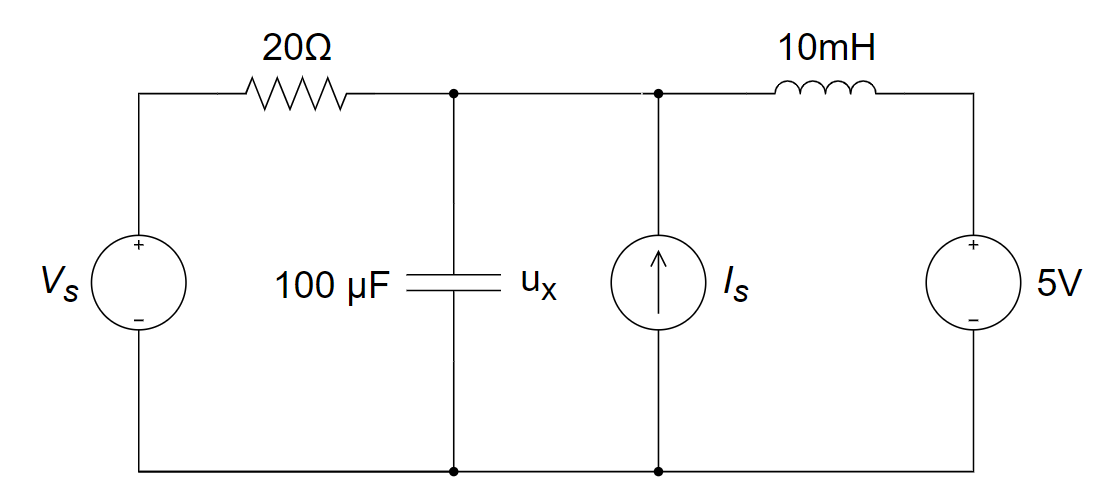
解析：

(1) 保留 5 V 的电压源，turn off 电流源和 电压源

​ 电路稳定后，电感等效于短路，故有：

(2) 保留电流源，turn off 两个电压源

​

​ 解得：

​

(3) 保留 电压源，turn off 电流源和 5 V 的电压源

​

​ 解得：

​

(4) 综上，

CH05-KP3-16: 用网孔电流法求解下图中的 。

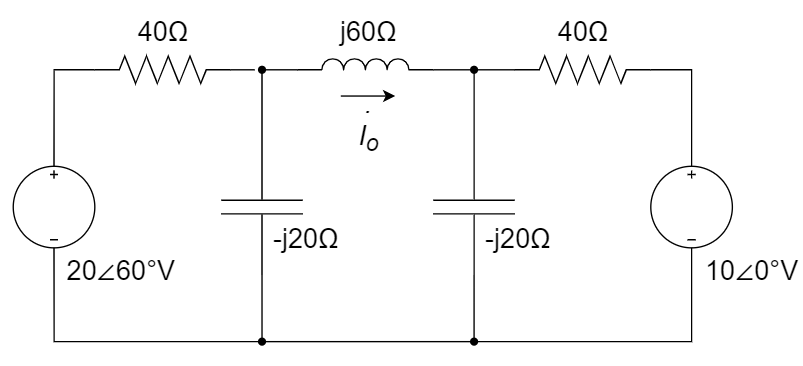
解析：

设三个网孔的电流从左往右依次为 、、，方向为顺时针。

则有网孔电流方程

计算得到

CH05-KP3-17: 如下图所示电路，设 ，，用节点电压法求 的稳态表达式。

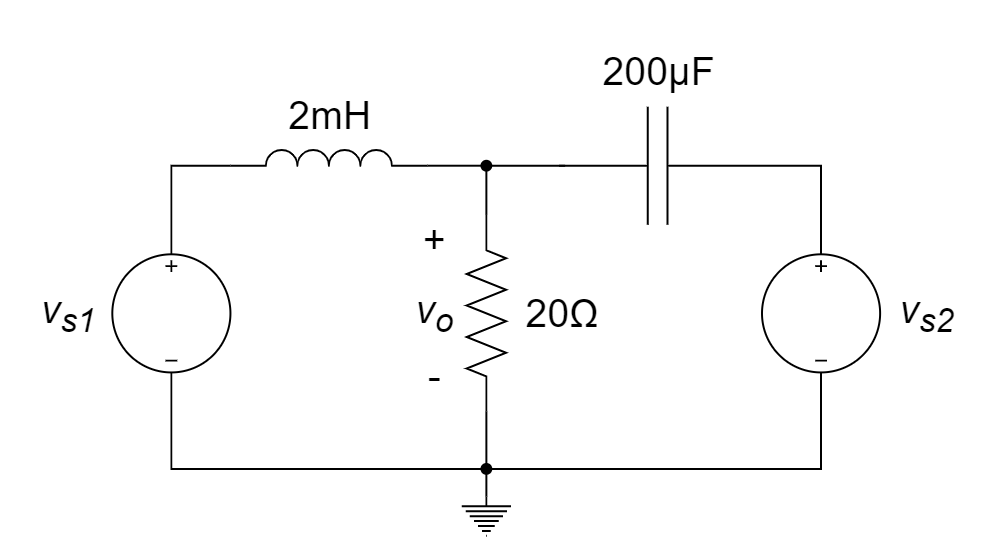
解析：

以底端节点作为参考节点，则上方节点电压为 。

列节点电压方程

其中，，代入 计算得：

CH05-KP3-18: 已知 = 10 mH， = 50 mF， = 100 mF，求正弦稳态电路中电容 两端的电压 。

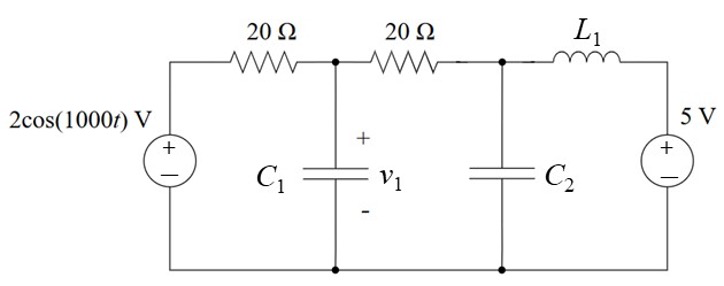
解析：

知识点4：其他

CH05-KP4-01: 下列哪种说法不正确？

A. 理想直流电流源的输出电流始终是一个定值，与它两端的电压无关

B. 双端网络的端口电压超前电流时，该网络一定是感性的

C. 受控源在电路分析中的作用和理想源相同，都可视为激励源看待

D. 戴维南定理和诺顿定理仅适用于线性电路

参考答案	C

解析：

受控源和独立源的对待方式不同，比如在求等效电阻时，独立源turn off，而受控源要保留