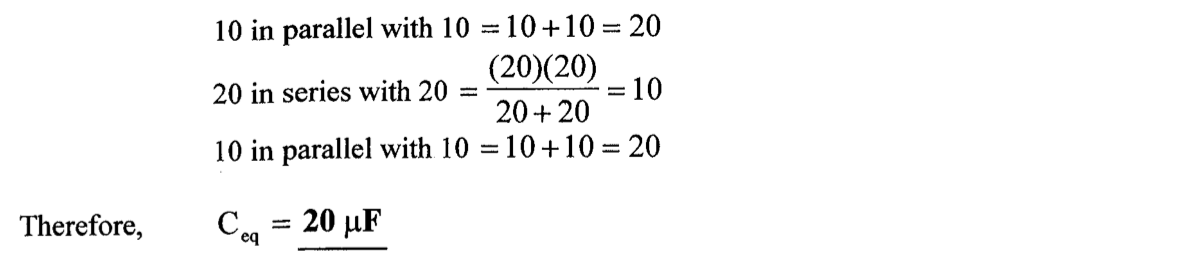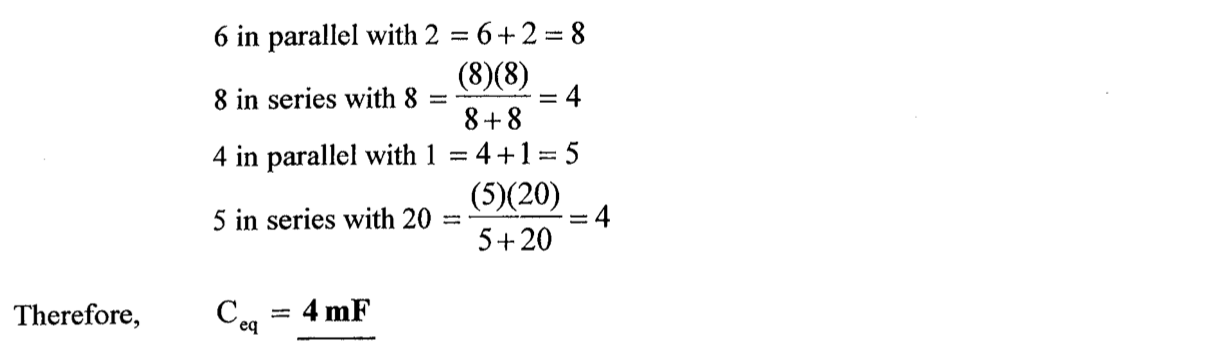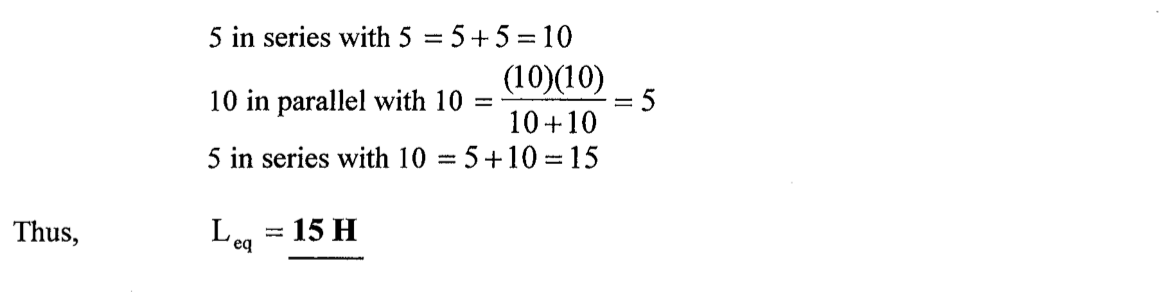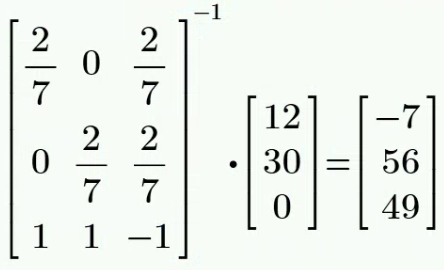电路的等效变换
INFO
2. 电路的等效变换(建议4学时)
2.1 电路等效
2.2 基尔霍夫电路定律
2.3 电阻电路的等效变换
2.3.1 电阻的串联和并联
2.3.2 电阻的混联和Y-∆等效变换
2.4 储能元件电路的等效变换
2.4.1 电容的串联和并联
2.4.2 电感的串联和并联
2.5 电源电路的等效变换
2.5.1 电压源的串联和并联
2.5.2 电流源的串联和并联
TIP
电路等效概念:接口处电压、电流保持不变;
电路等效计算,即输入电阻/等效电阻计算(针对一端口网络)
若仅含电阻,等效化简即可;
若含受控源,但不含独立源,施加电压求电流,或者施加电流求电压;
若含独立源,则先将其 turn off(电压源短路,电流源开路),再计算;
KCL的两种表述
- 流入任一节点(或闭合界面)的支路电流的代数和为0;电荷守恒;
- 对于任一节点,流入电流总和 = 流出电流总和;
KVL的两种表述
- 沿任一回路,所有支路电压的代数和为0;能量守恒;
- 两节点间若有多条路径,则每条路径上的电压降相等(电压与路径无关);
电阻电路的分析
- 串联分压,总电阻为各电阻之和;并联分流,总电导为各电导之和;
- Weatstone电桥:平衡时电阻成比例,流过电流计电流为零;
电容电感串并联
电感类似于电阻,串联则电感值相加,并联则电感值的倒数相加;
电容并联则电容值相加,类似于电阻串联;电容串联则电容值倒数相加,类似于电阻并联
Y-Δ等效变换
to Y: Y to
: 阻值比较大,更像并联;Y 阻值比较小,更像串联;当阻值相等时,
电源变换。”电压源串联电阻“ 等价于 ”电流源并联电阻“
习题及参考解答
知识点1: 电路等效及相关计算
CH02-KP1-01: 右图所示电路的等效电阻为 ________ 。
A. 4 Ω
B. 1 Ω
C. ﹣2 Ω
D. 2 Ω
| 参考答案 | C |
|---|
解析:
根据 KCL,从上往下流过下面 2 ohm 电阻的电流为
,据此,可写出端口电压为 ;等效电阻为端口电压除以端口电流,故为 。
CH02-KP1-02: 右图所示电路的等效电阻
| 参考答案 |
|---|
解析:
, 。
CH02-KP1-03: 理想电压源和理想电流源串联,其等效电路为 ________ 。
| 参考答案 | 电流源 |
|---|
解析:
与理想电压源并联的元件无效(因为其电压仍由理想电压源决定);与理想电流源串联的元件无效(因其电流仍由理想电流源决定);题中为串联,故等效电路为电流源。
CH02-KP1-04: 右图的等效电容为 ________ 。
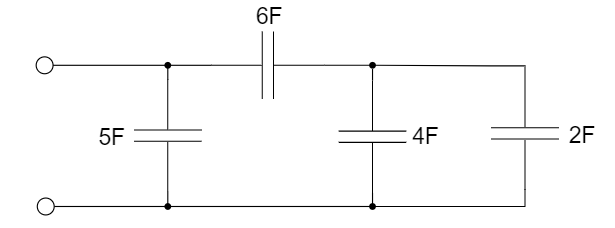
| 参考答案 | 8 F |
|---|
解析:
电容并联相当于电阻串联;电容串联相当于电阻并联;所以,4 F || 2 F = 6 F, 6 F 串联 6 F = 3 F, 3 F || 5 F = 8 F
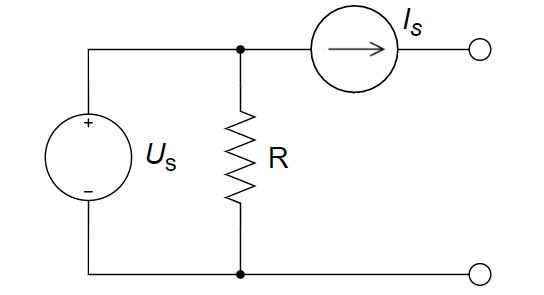
CH02-KP1-05: 右图所示电路的等效电路为 ________ 。
A. 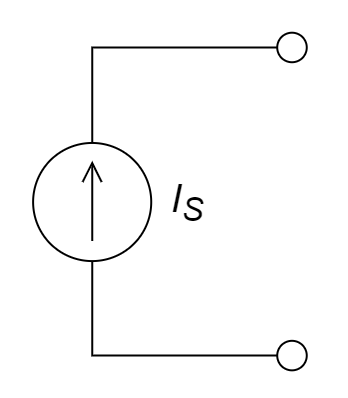
B. 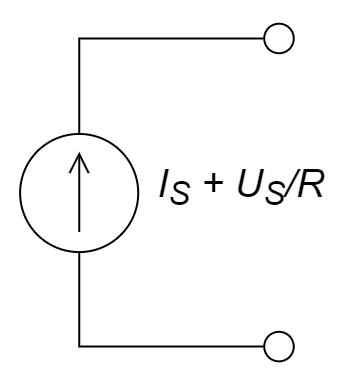
C. 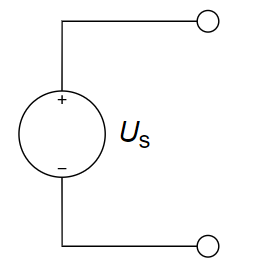
D. 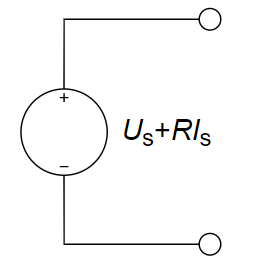
| 参考答案 | A |
|---|
解析:
与理想电压源并联的电阻无效,故第一步简化为理想电压源和理想电流源串联;与理想电流源串联的元件无效,故第二步简化为单个的理想电流源,所以答案为 A。
CH02-KP1-06: 下图所示电路 ab 端的等效电阻
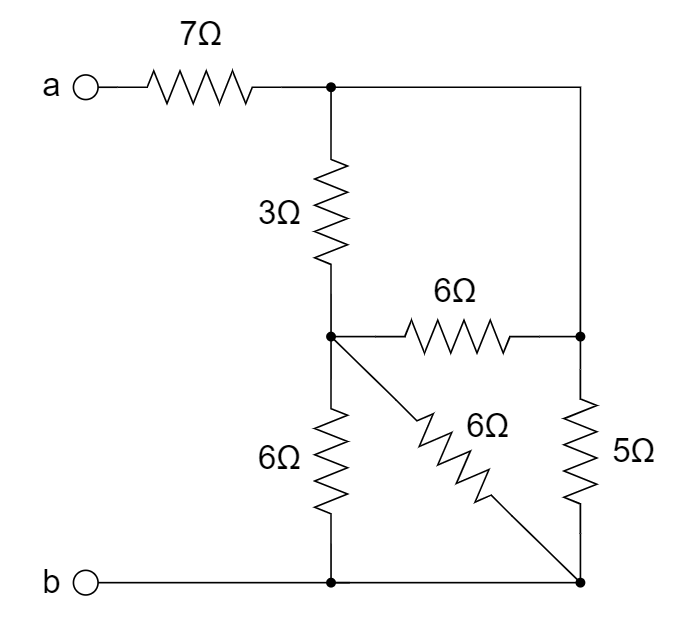
A. 10 Ω
B. 9.5 Ω
C. 9 Ω
D. 8.5 Ω
| 参考答案 | B |
|---|
解析:
右上方的 3 ohm 和 6 ohm 并联,等效为 2 ohm;下方的两个 6 ohm 并联,等效为 3 ohm;2 ohm 和 3 ohm 串联再和 5 ohm 并联,等效为 2.5 ohm,再和 7 ohm 串联,等效为 9.5 ohm。
CH02-KP1-07: 下图所示电路的端口等效电阻等于 ________ Ω。
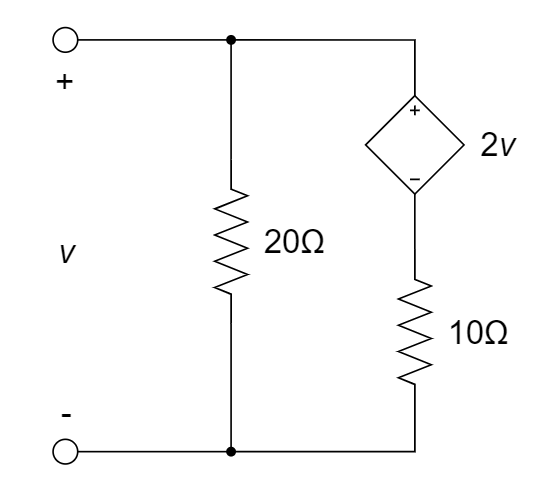
| 参考答案 |
|---|
解析:
10 ohm上的电压降为
,故电流从上往下为 ,20 ohm 电流从上往下为 ,所以端口电流为 ,等效电阻为端口电压除以端口电流 = 。
CH02-KP1-08: 求下图的等效电容
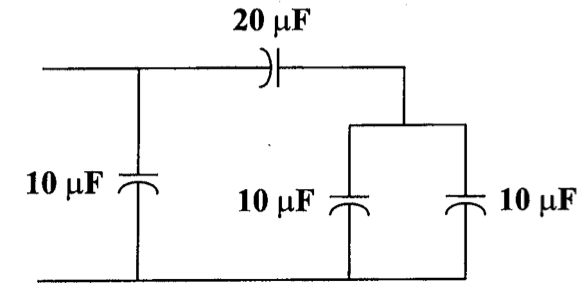
| 参考答案 |
|---|
解析:
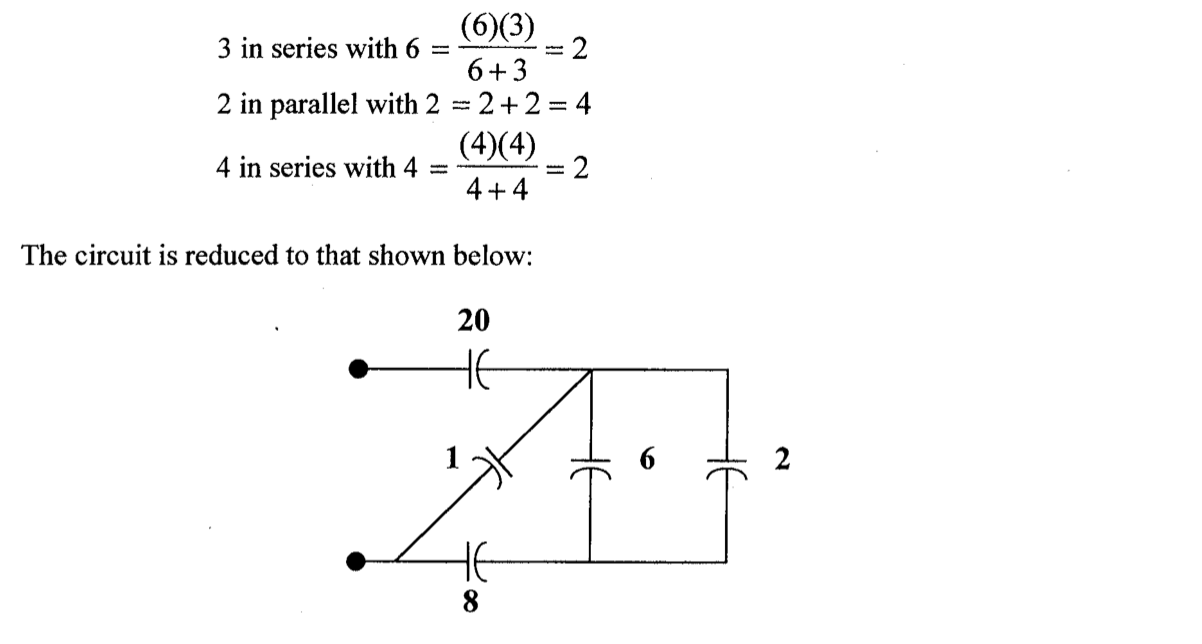
CH02-KP1-09: 求下图的等效电容,图中电容值的单位为 mF。
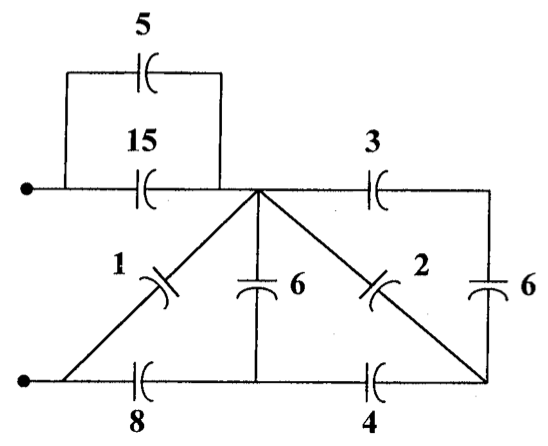
| 参考答案 | 4 mF |
|---|
解析:
CH02-KP1-10: 求下图的等效电感
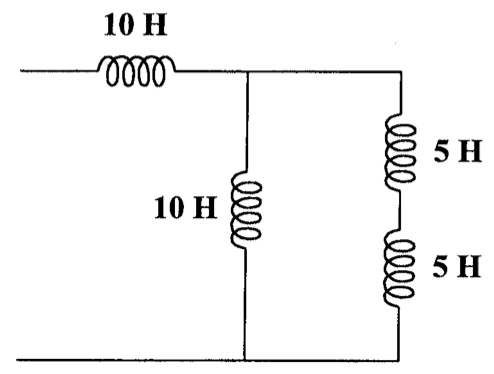
| 参考答案 | 15 H |
|---|
解析:
CH02-KP1-11: 右图所示电路的端口等效电阻
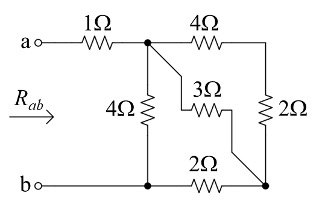
| 参考答案 |
|---|
解析:
右上角 4 ohm 和 2 ohm 串联等效为 6 ohm; 再与 3 ohm 并联,等效为2 ohm;再与 2 ohm 串联,等效为 4 ohm; 再与 4 ohm 并联,等效为 2 ohm;最后再与 1 ohm 串联,等效为 3 ohm。
知识点2:基尔霍夫定律
CH02-KP2-01: 基尔霍夫电压定律和电流定律的本质分别是 ________ 。
A. 电荷守恒和能量守恒
B. 电荷守恒和电荷守恒
C. 能量守恒和能量守恒
D. 能量守恒和电荷守恒
| 参考答案 | D |
|---|
解析:
KVL 的本质是能量守恒,因为电压的本意是移动单位电荷所需做的功;KCL 的本质是电荷守恒,因为电流的本意是单位时间内流过某一截面(或某一节点)的电荷量。
CH02-KP2-02: 基尔霍夫电流定律(KCL)是电流连续性的表现,其本质是 ________ ,基尔霍夫电压定律(KVL)本质是 ________ 。
| 参考答案 | 电荷守恒;能量守恒 |
|---|
解析:
同
CH02-KP2-01
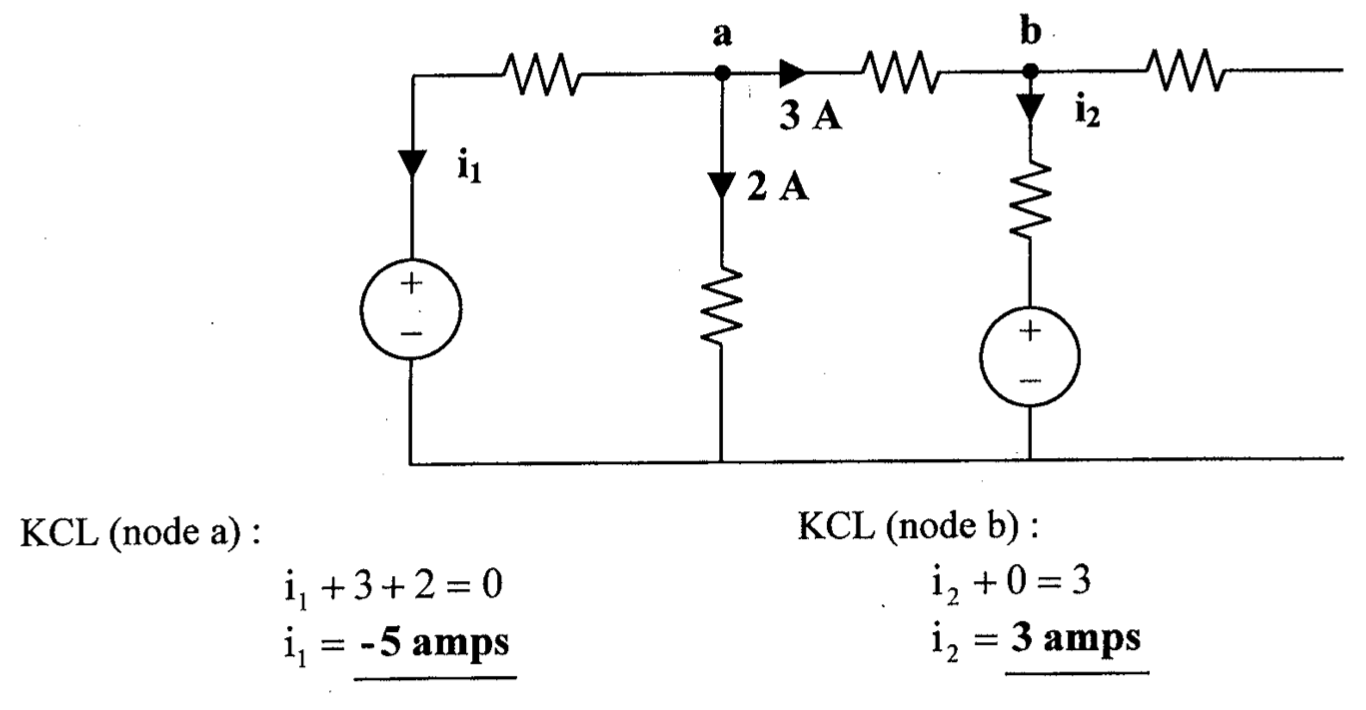
CH02-KP2-03: 下图中的电流
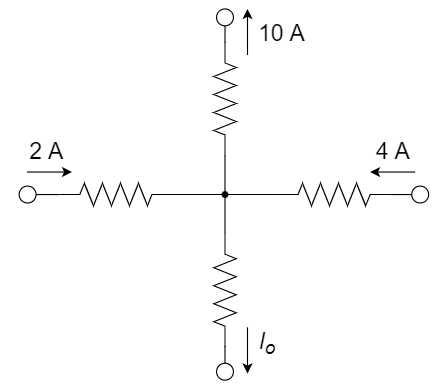
A. 4 A
B. 16 A
C.
D.
| 参考答案 | C |
|---|
解析:
流入电流(2+4)= 流出电流(10+
),所以
CH02-KP2-04: 分析电路,求
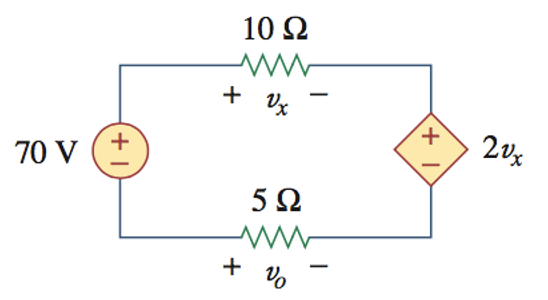
| 参考答案 |
|---|
解析:
从左下角开始,顺时针写 KVL 方程,约定遇到元件的 "
CH02-KP2-05: 分析电路,求
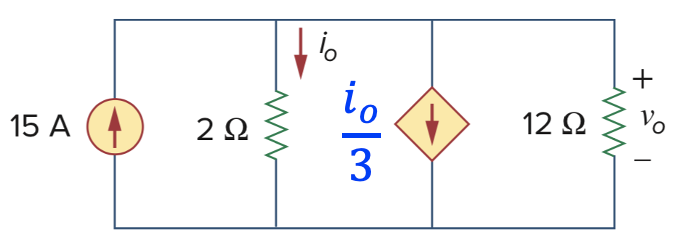
| 参考答案 |
|---|
解析:
CH02-KP2-06: 分析电路,求图中标示的所有电压电流
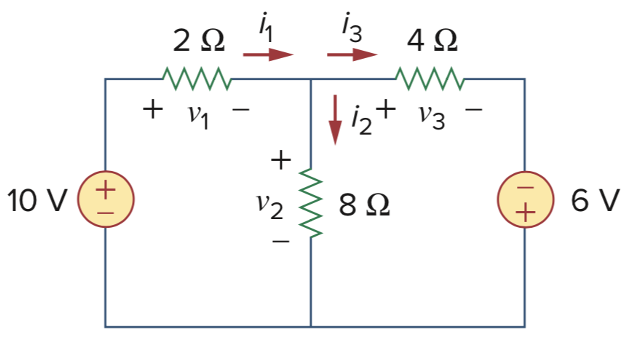
| 参考答案 | |
|---|---|
| SPICE仿真 | 仿真文件见 Github spice/ch02/CH02-KP2-06.kicad_sch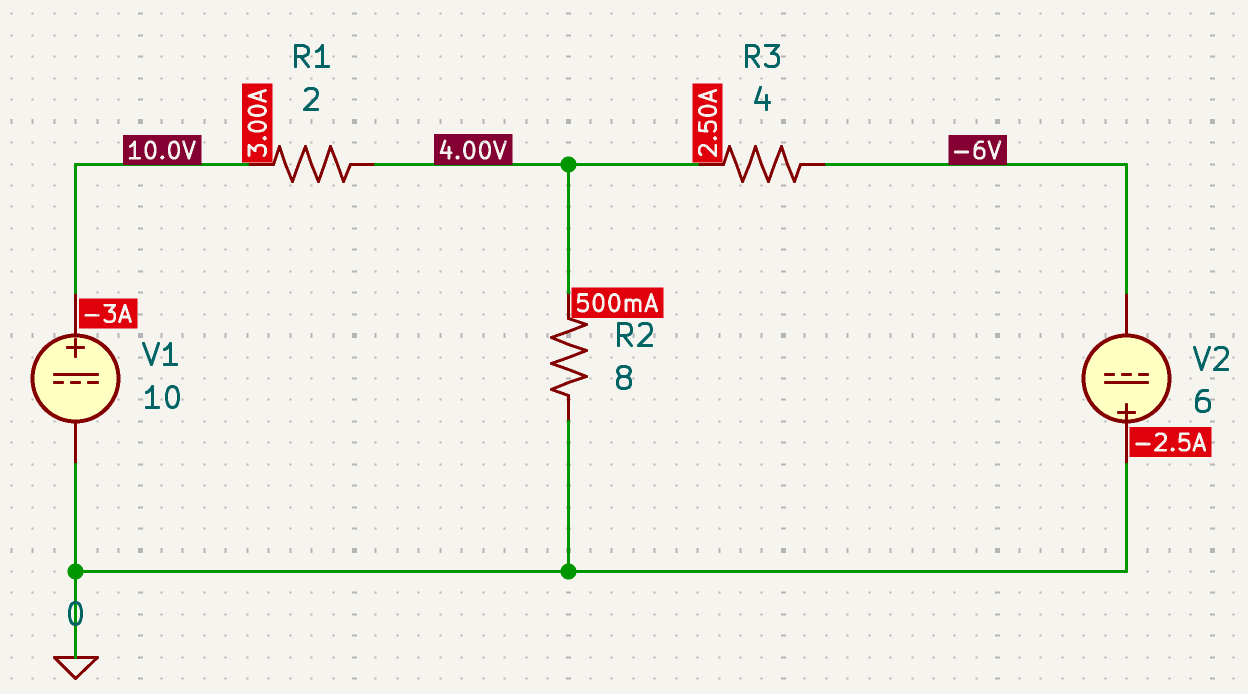 |
| Math | 数学计算文件见 Github math/ch02/CH02_KP2_06.m |
解析:
CH02-KP2-07: 求下图中的
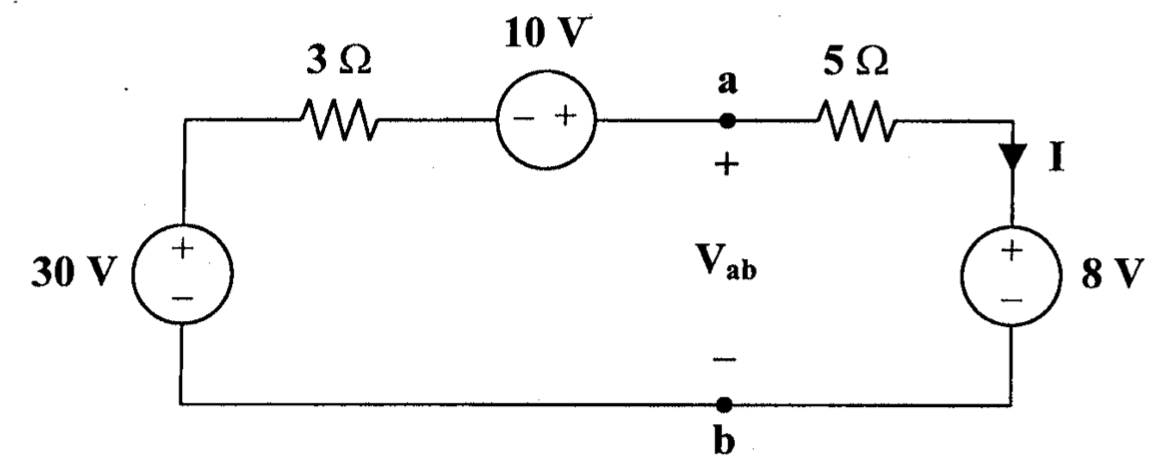
| 参考答案 | |
|---|---|
| SPICE仿真 | 仿真文件见 Github spice/ch02/CH02-KP2-07.kicad_sch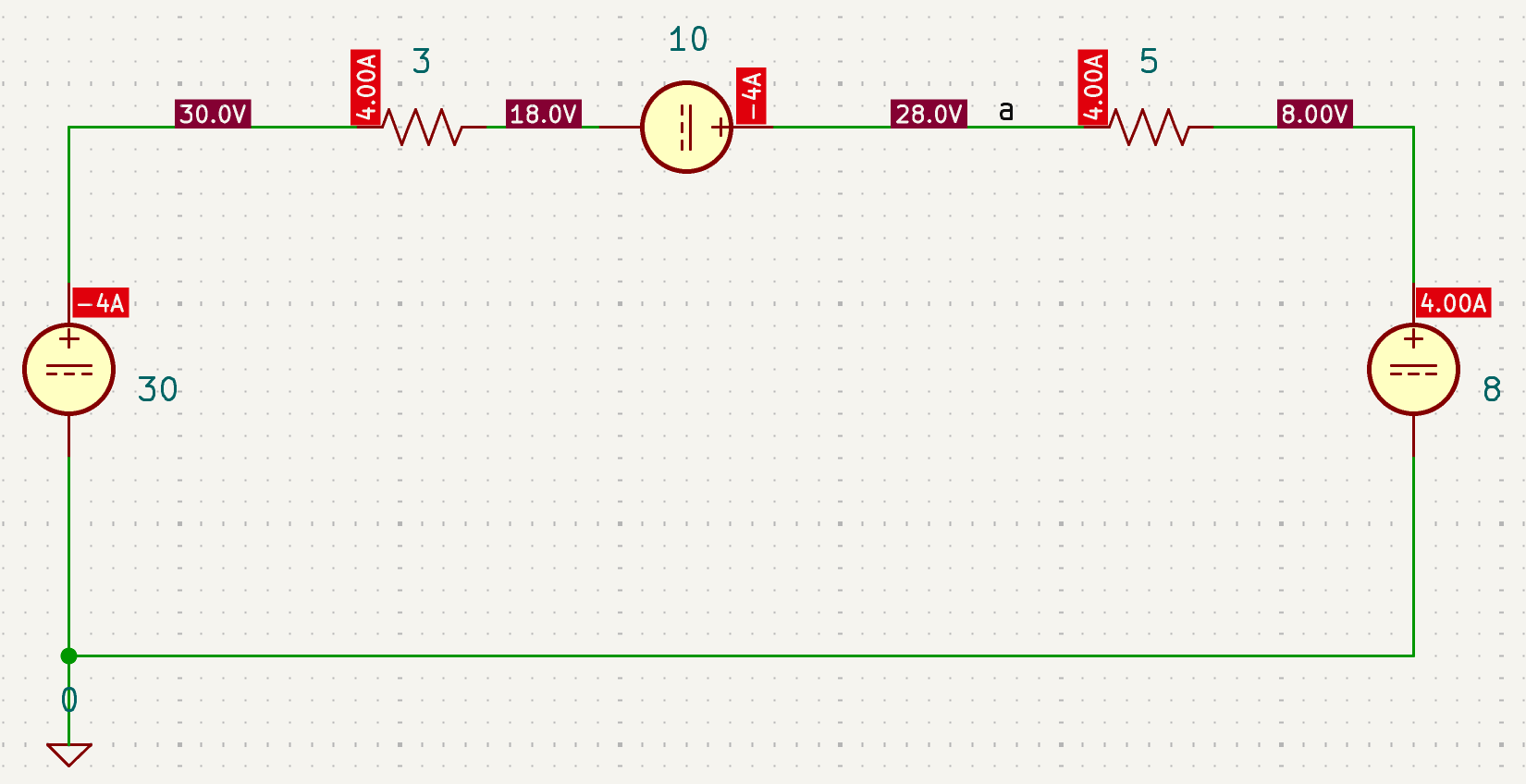 |
解析:
CH02-KP2-08: 求下图中的
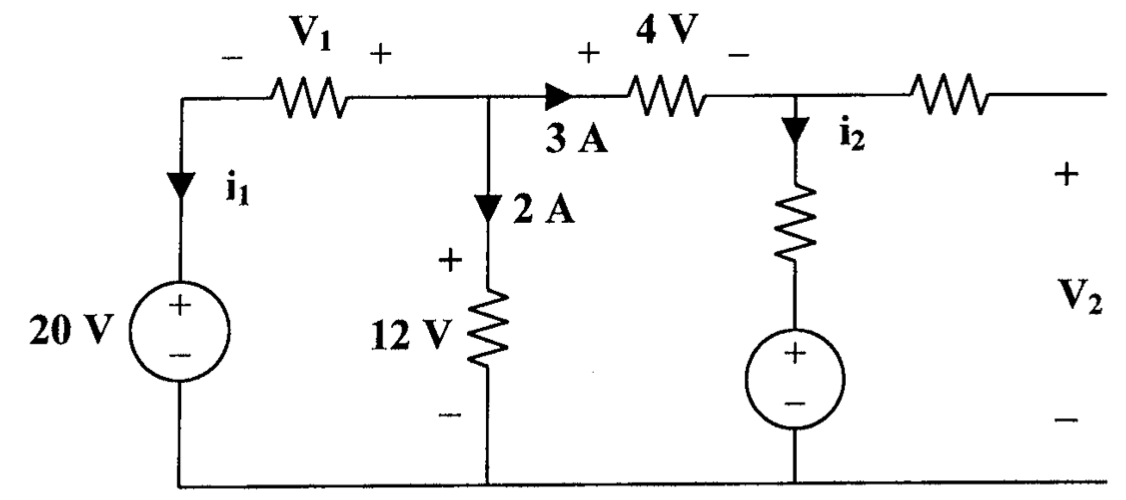
| 参考答案 |
|---|
解析:
知识点3:电阻电路的分析
CH02-KP3-01: 下图中,电流
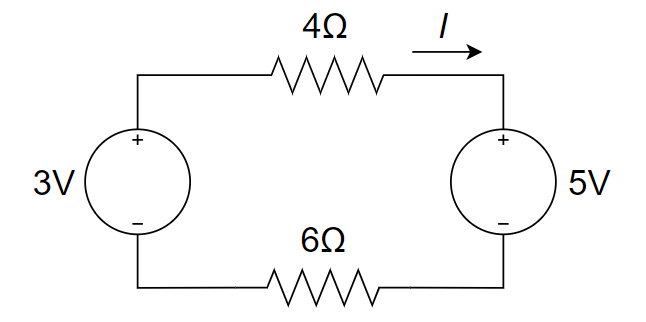
| 参考答案 |
|---|
解析:
列 KVL 方程,
CH02-KP3-02: 计算下图中的
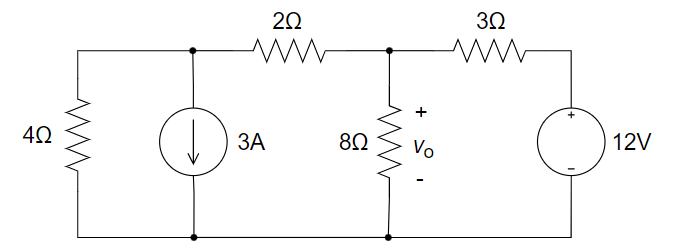
| 参考答案 | 3.2 V |
|---|---|
| SPICE仿真 | 仿真文件见 Github spice/ch02/CH02-KP3-02.kicad_sch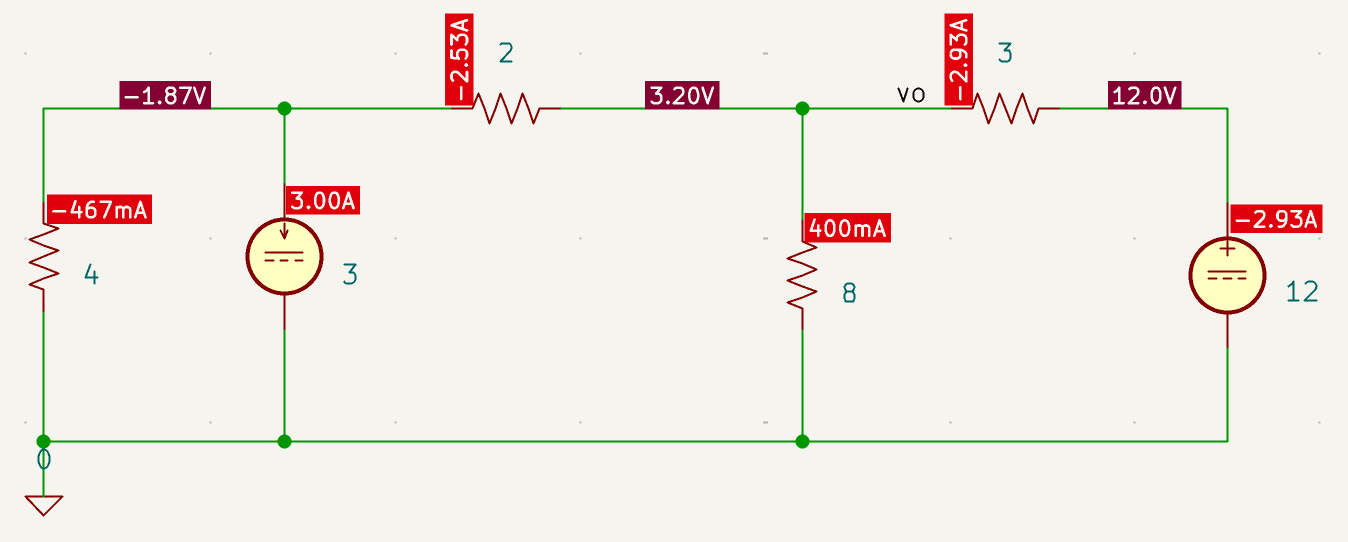 |
解析:
设左边节点电压为 va,对其用 KCL 方程,则,va/4 + 3 + (va-vo)/2 = 0; 对中间这个节点也用KCL,则 (va-vo)/2 = vo/8 + (vo-12)/3;联立两个方程,可求出 v0 = 48/15 = 3.2 V
CH02-KP3-03: 下图所示电路中,电压 U 为 ________ 。
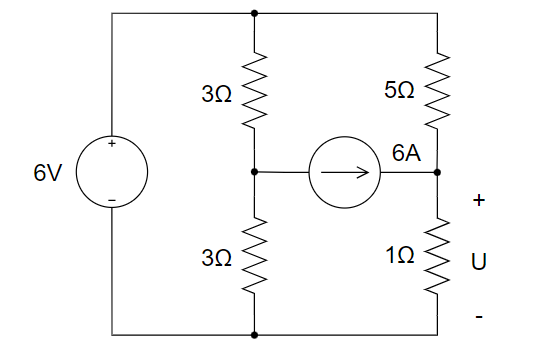
A. 4V
B. 5V
C. 6V
D. 3V
| 参考答案 | C |
|---|---|
| SPICE仿真 | 仿真文件见 Github spice/ch02/CH02-KP3-03.kicad_sch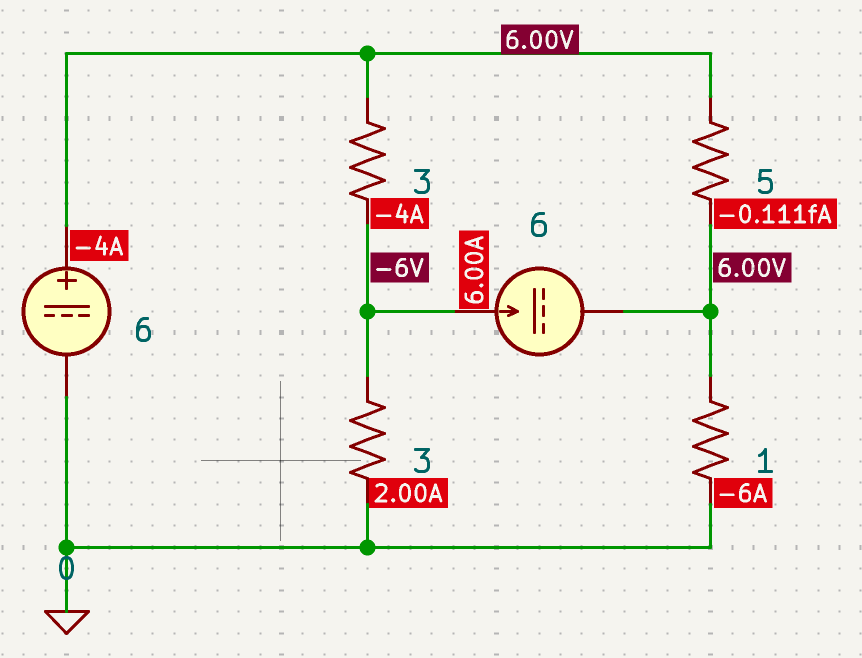 |
解析:
对右边中间节点列 KCL,则 (6-U)/5 + 6 = U/1,解得 U= 6 V
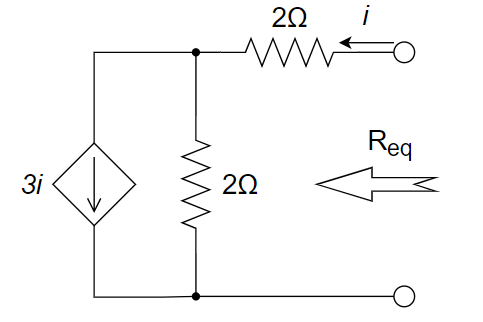
CH02-KP3-04: 下图中受控电流源的转移电导
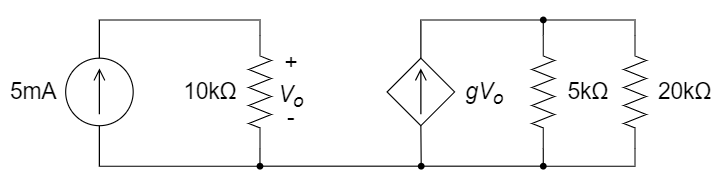
| 参考答案 | 2 V |
|---|---|
| SPICE仿真 | 仿真文件见 Github spice/ch02/CH02-KP3-04.kicad_sch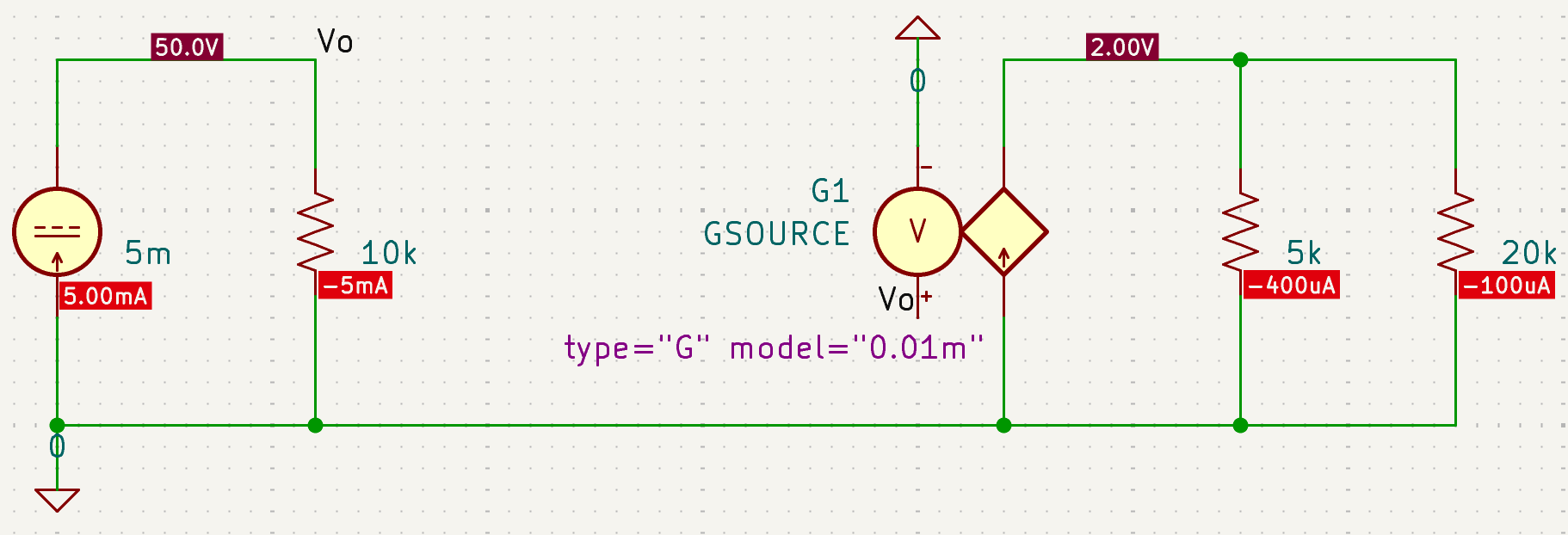 |
解析:
, ,两个电阻分流,20 kohm上流过的电流为0.1 mA,故其两端电压为 2 V。
CH02-KP3-05: Wheatstone 电桥广泛应用于电阻测量,已知待测电阻
(a) 该同学的设计思路是什么(即如何实现电阻测量)?
(b)
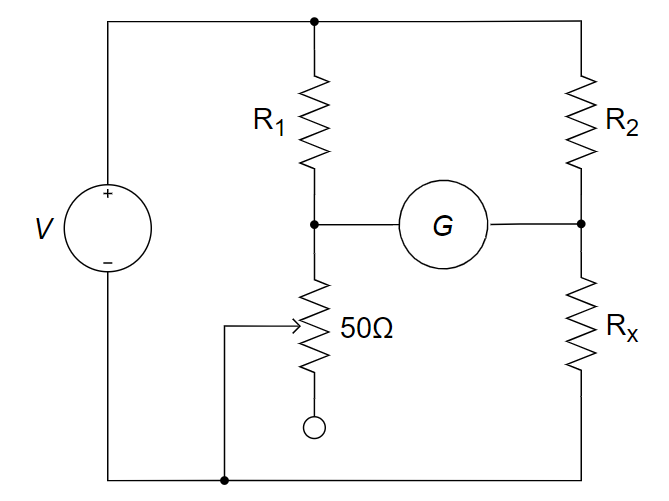
| 参考答案 | (a) 调节 50 Ω 变阻器,当电桥平衡(电流计电流为0)时,通过比值关系获得待测电阻 |
|---|
解析:
略
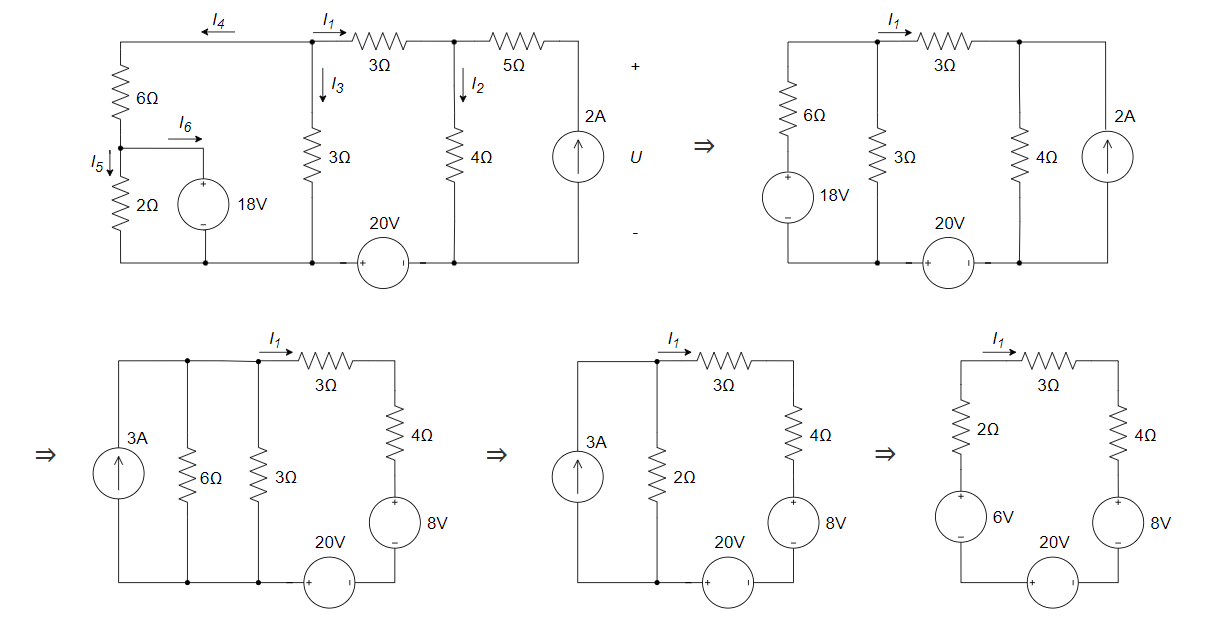
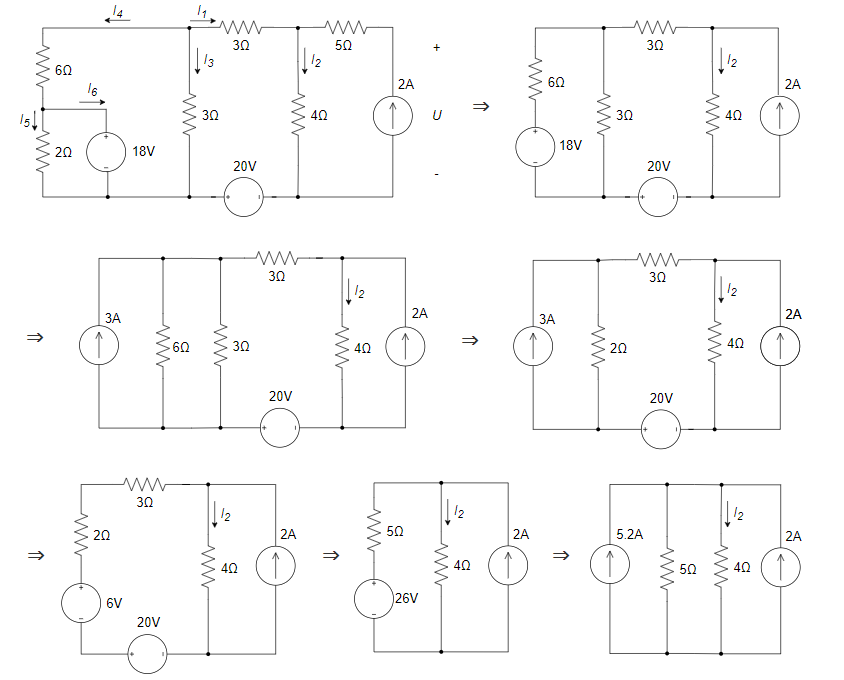
CH02-KP3-06: 求下图所示电路中电流
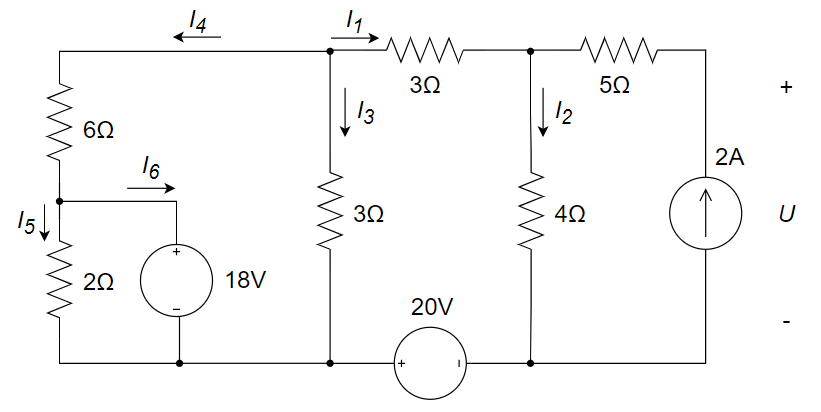
| 参考答案 | |
|---|---|
| SPICE仿真 | 仿真文件见 Github spice/ch02/CH02-KP3-06.kicad_sch |
| Math | 数学计算文件见 Github math/ch02/CH02_KP3_06.m |
解析:
方法一:
根据各电流量之间的关系、18 V 和 20 V 电压源在负载上的电压降关系,以及左侧大回路的回路电压降关系,列方程组如下:
解得:
20 V 电压源的功率为:
,发出功率 2 A 电流源的功率为:
,发出功率 18 V 电压源的功率为:
,发出功率 方法二:
(1) 等效电路
得:
20 V 电压源的功率为
,发出功率 (2) 等效电路
得:
原电路
2 A 电流源的功率为
,发出功率 (3) 18 V 电压源的功率为
,发出功率
CH02-KP3-07: 欲使下图所示电路中的支路电流
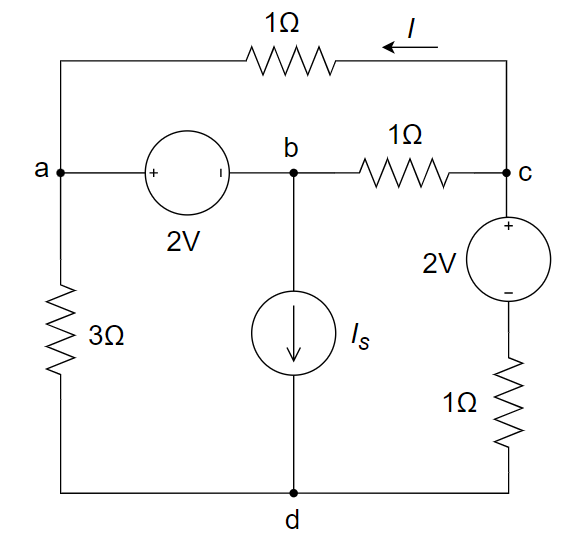
| 参考答案 | 5 A |
|---|---|
| SPICE仿真 | 仿真文件见 Github spice/ch02/CH02-KP3-07.kicad_sch |
解析:
CH02-KP3-08: 如下图所示电路,支路电流
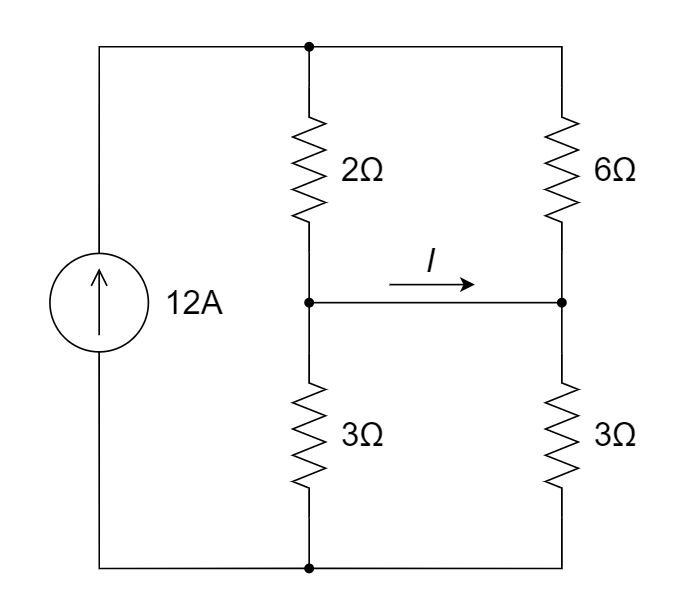
| 参考答案 | 3 A |
|---|---|
| SPICE仿真 | 仿真文件见 Github spice/ch02/CH02-KP3-08.kicad_sch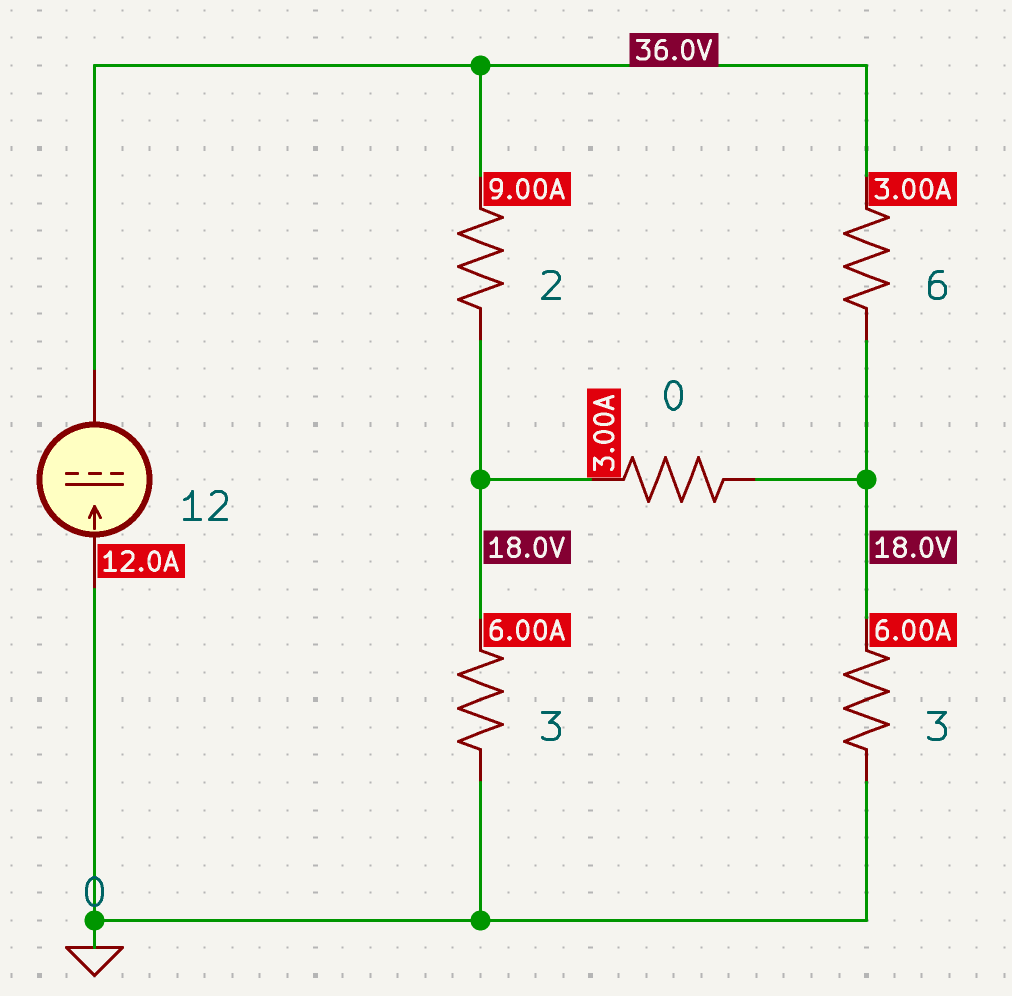 |
解析:
上方两个电阻分流,流过 2 ohm 的电流为 9 A;下方两个电阻分流,流过左边 3 ohm 的电流为 6 A,所以 I=3A
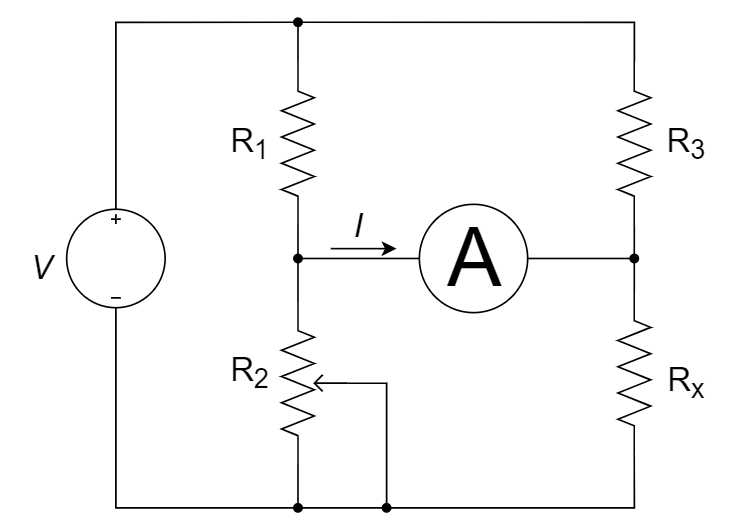
CH02-KP3-09: 利用如下图所示的惠斯登电桥可以较为精确地测量中等阻值的电阻,其中
| 参考答案 |
|---|
解析:
电桥平衡时,电阻呈比例,R1:R3 = 1:1 = R2:Rx, 所以 Rx=4ohm
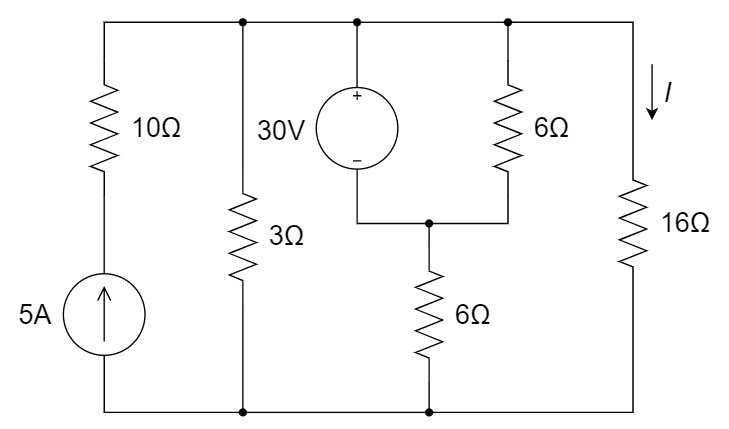
CH02-KP3-10: 下图所示电路中,电流
| 参考答案 | |
|---|---|
| SPICE仿真 | 仿真文件见 Github spice/ch02/CH02-KP3-10.kicad_sch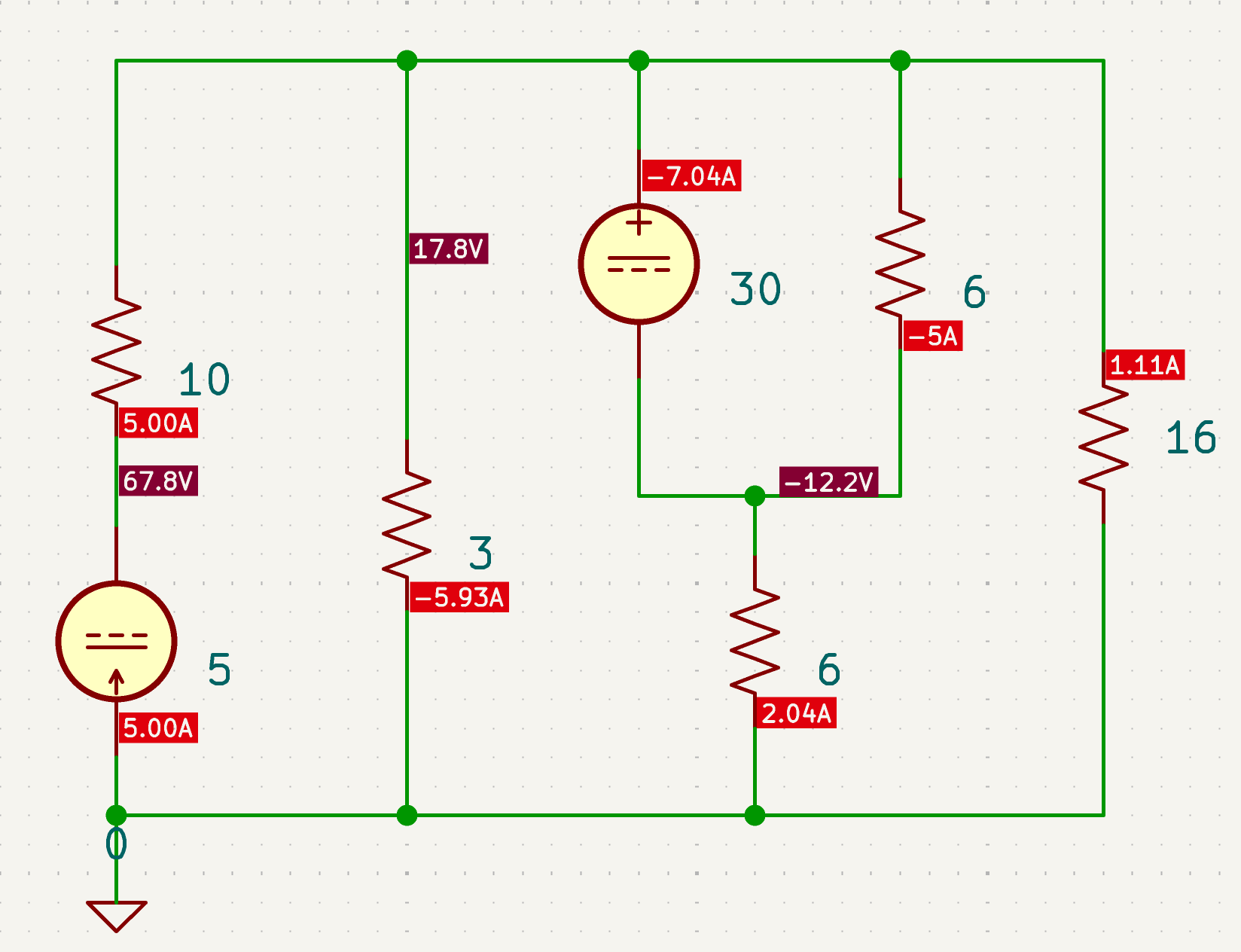 |
解析:
与电流源串联的电阻不改变电流值;与电压源并联的电阻不改变电压值。设中间节点电压为 vx,对最上方节点列 KCL: 5 = (vx + 30)/3 + vx/6 + (vx + 30)/16, 可解出 vx=-110/9 V,进一步计算出 I= (30-110/9)16 =10/9 A
CH02-KP3-11: 根据图中的参数,计算
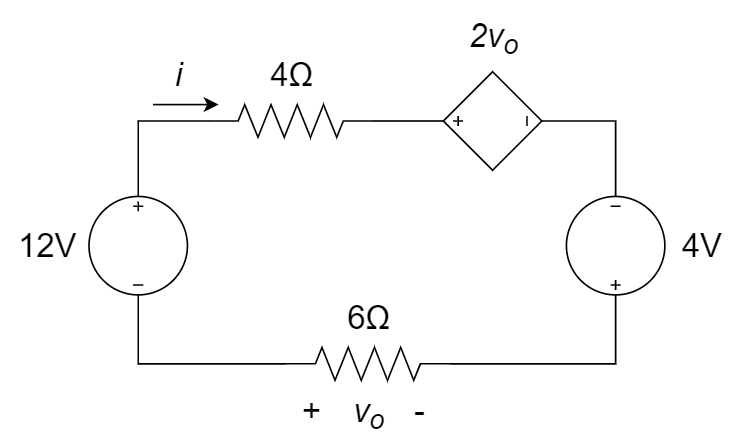
| 参考答案 | 48 V |
|---|---|
| SPICE仿真 | 仿真文件见 Github spice/ch02/CH02-KP3-11.kicad_sch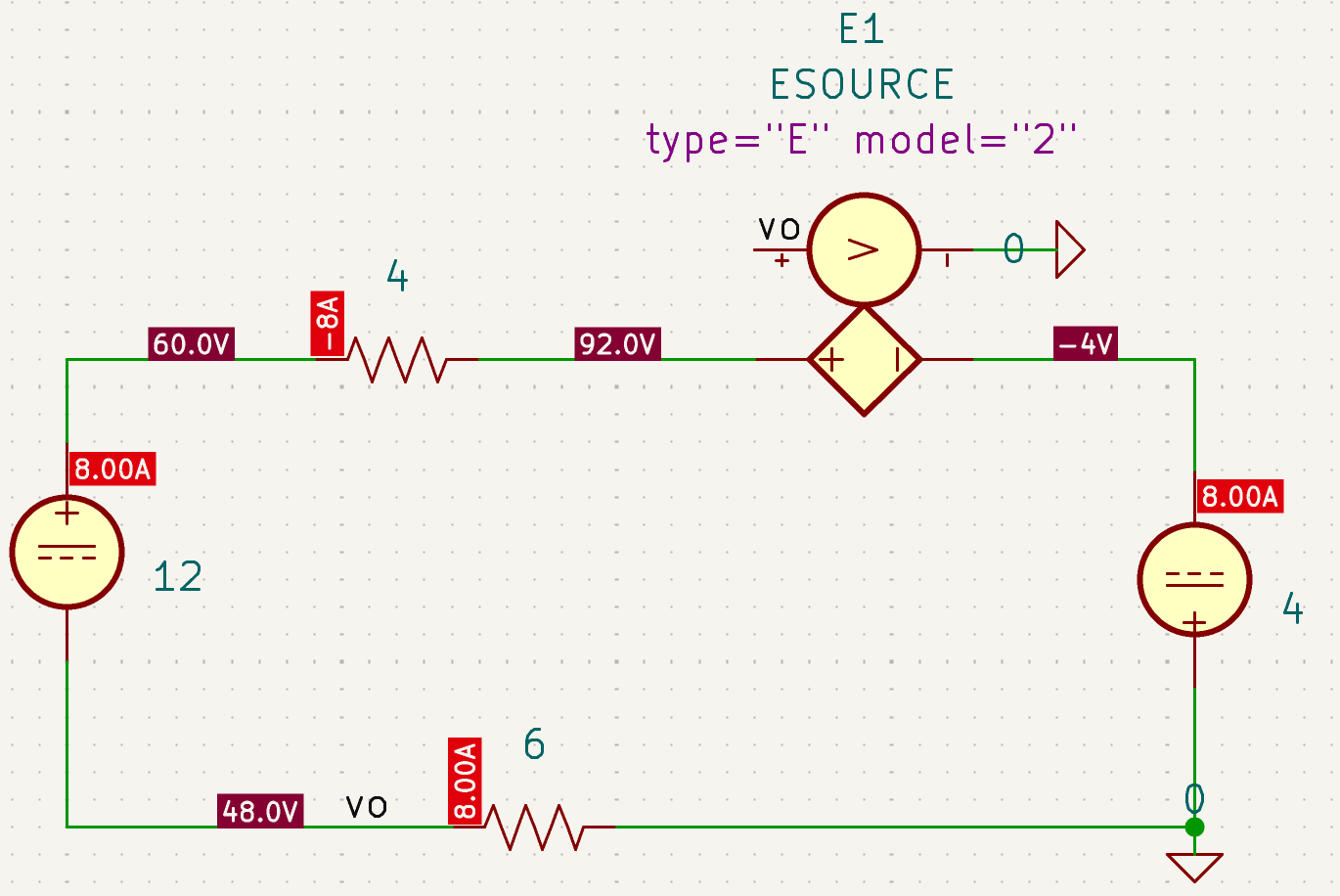 |
解析:
列方程组如下
CH02-KP3-12: 下图所示的电路中的
(1) 电流源的输出电流
(2) 30 Ω 电阻上消耗的功率;
(3) 100 V 电压源提供的功率。
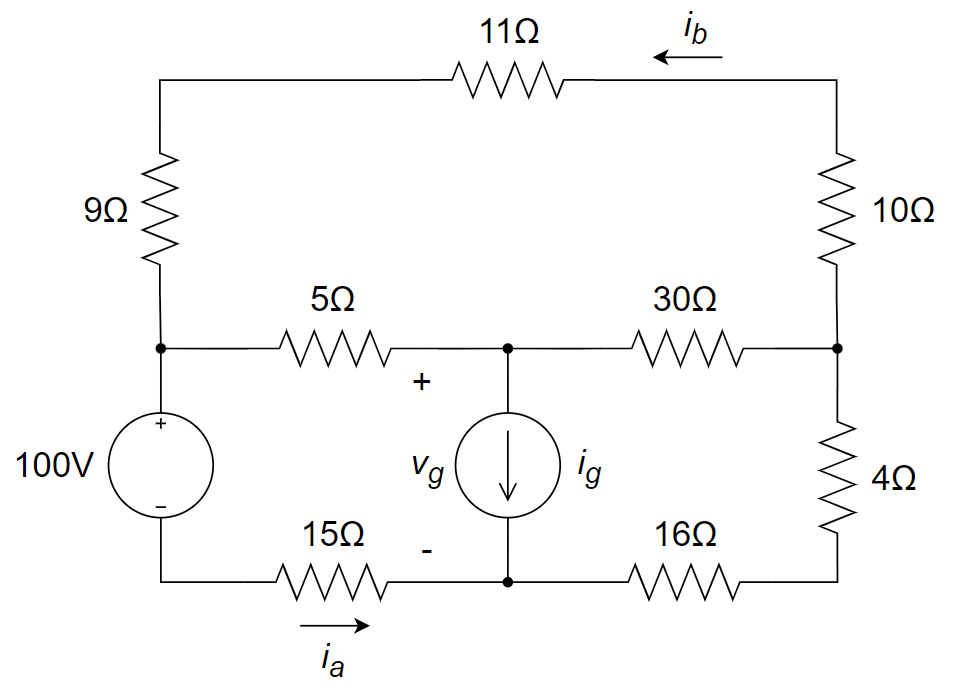
| 参考答案 | (1) |
|---|
解析:
(1)
;
;
(2)
(3) 按关联参考方向,
,所以电源吸收功率 400 W。
知识点4:Y-
CH02-KP4-01: 已知电路中
A. 40 Ω、40 Ω、40 Ω
B. 360 Ω、360 Ω、360 Ω
C. 120 Ω、120 Ω、120 Ω
D. 360 Ω、360 Ω、40 Ω
| 参考答案 | A |
|---|
解析:
阻值相等时,delta 电阻是 Y 电阻的三倍,所以为 40 ohm
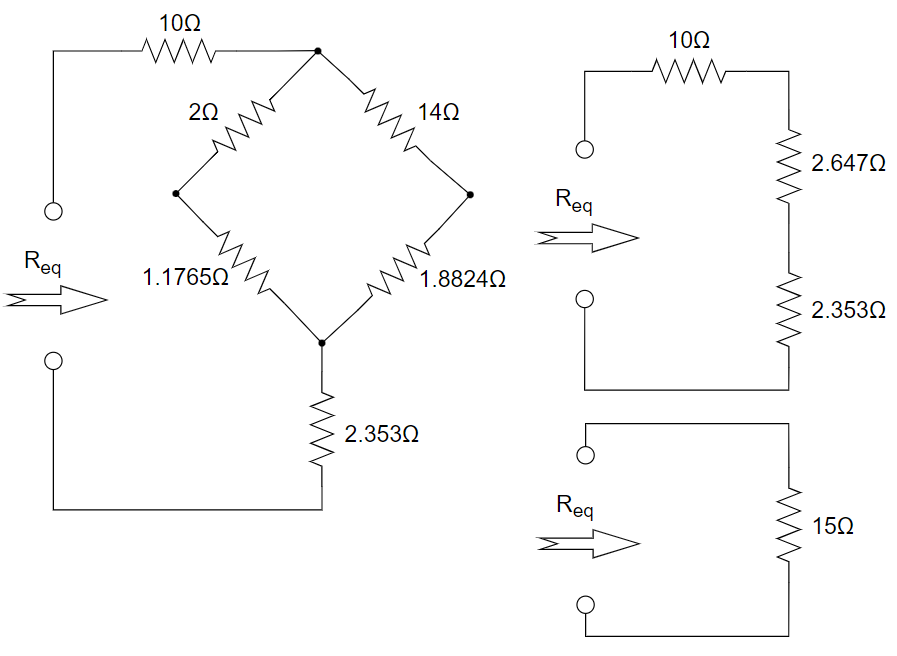
CH02-KP4-02: 求下图电路的等效电阻
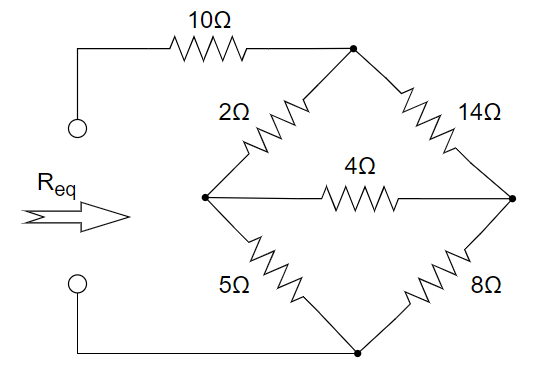
| 参考答案 | 15 Ω |
|---|
解析:
CH02-KP4-03: 求下图所示电路中的支路电流
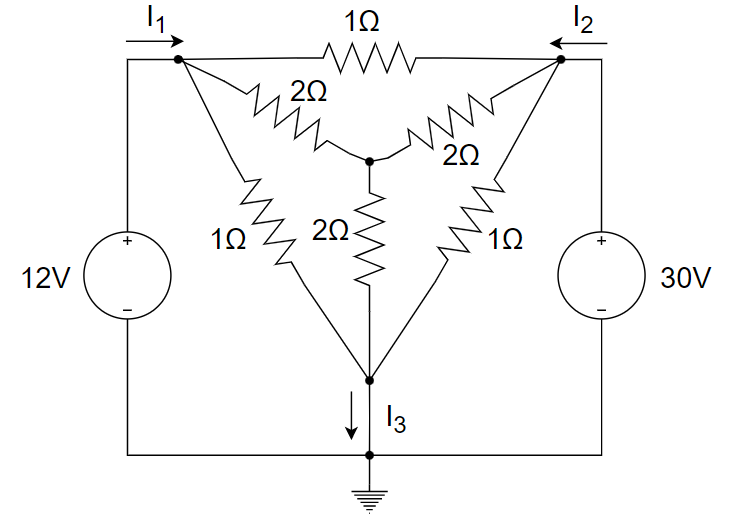
| 参考答案 | |
|---|---|
| SPICE仿真 | 仿真文件见 Github spice/ch02/CH02-KP4-03.kicad_sch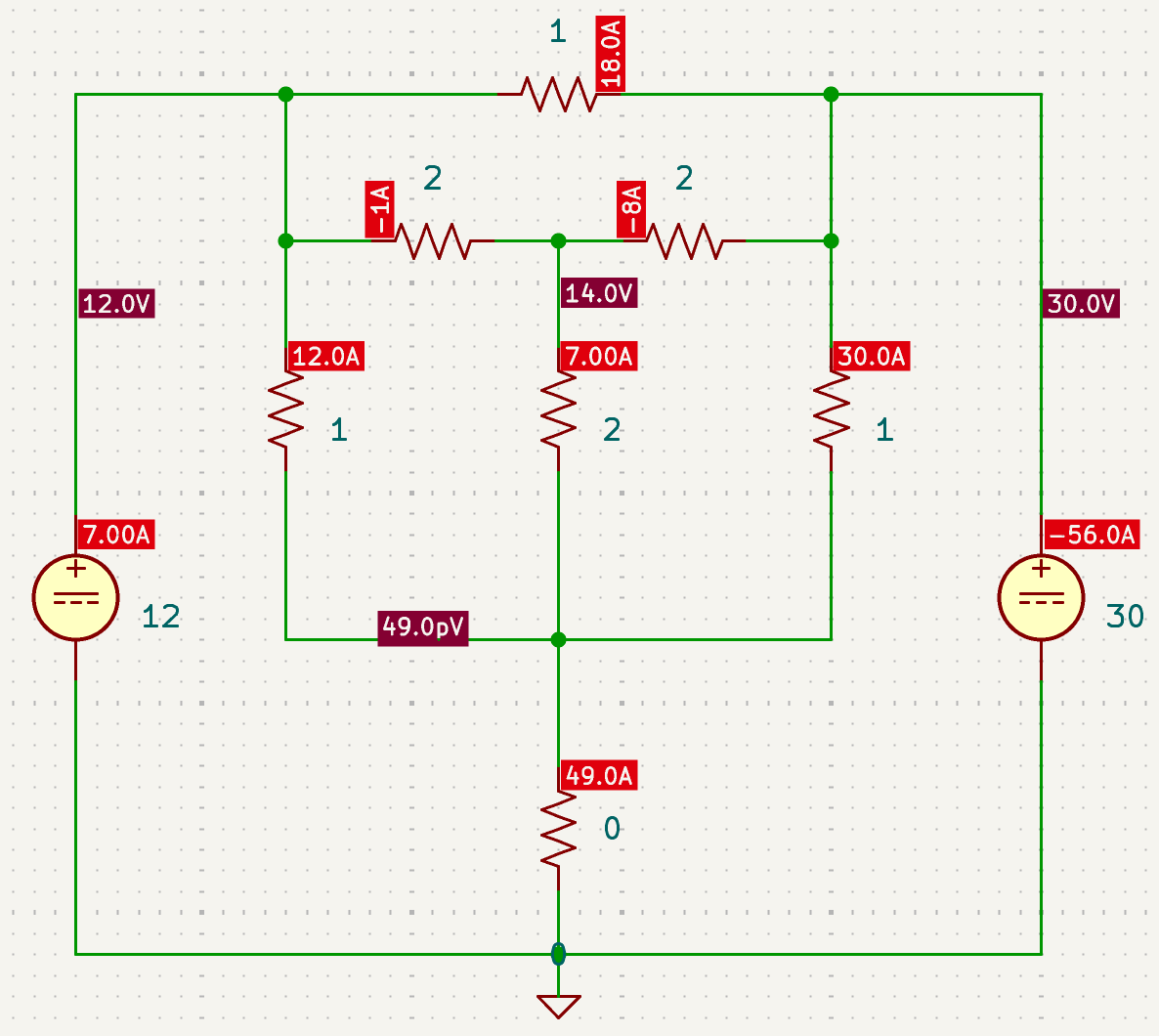 |
| Math | 数学计算文件见 Github math/ch02/CH02_KP4_03.m |
解析:
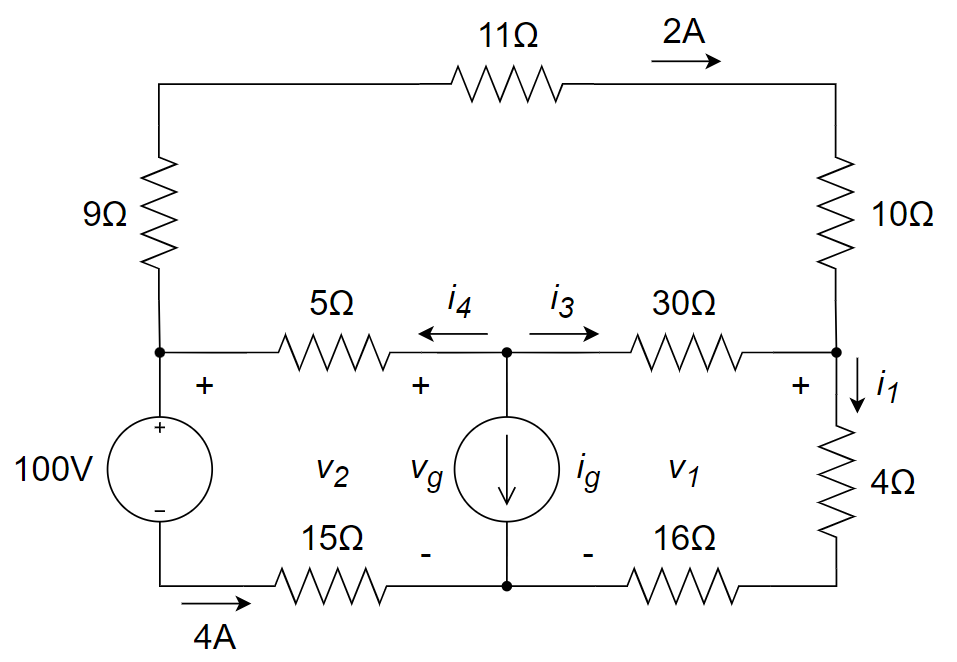
首先
变换为 ; 与 并联得到 ;在 转换得到 。 通过叠加定理或者网孔电流法可计算得到:
CH02-KP4-04: 分析电路,求
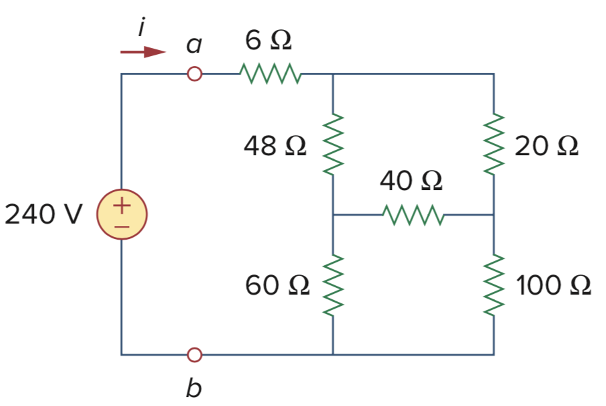
| 参考答案 | |
|---|---|
| SPICE仿真 | 仿真文件见 Github spice/ch02/CH02-KP4-04.kicad_sch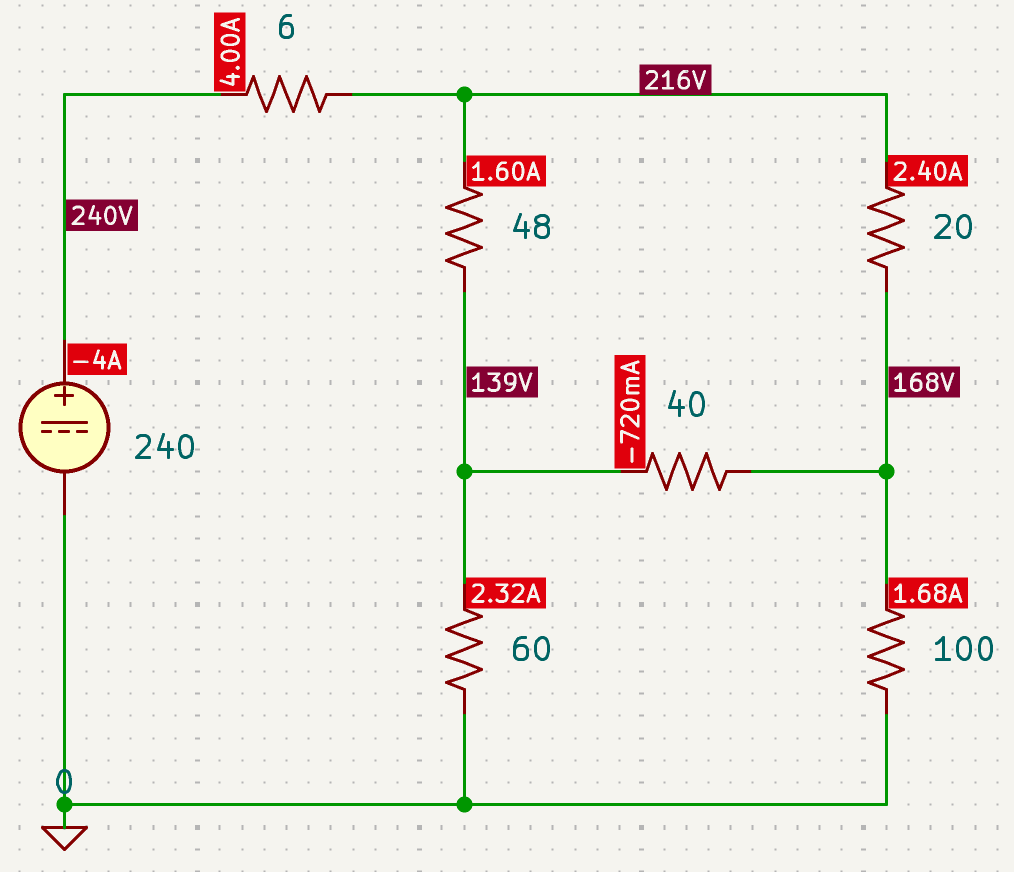 |
解析:
CH02-KP4-05: 已知 Δ 形电路中三个电阻均为 60 Ω ,那么转换后的 Y 形电路中的三个电阻分别为_________。
A. 60 Ω、60 Ω、60 Ω
B. 180 Ω、180 Ω、180 Ω
C. 20 Ω、20 Ω、20 Ω
D. 180 Ω、180 Ω、20 Ω
| 参考答案 | C |
|---|
解析:
阻值相等时,delta 电阻是 Y 电阻的三倍
知识点5:储能电路分析
CH02-KP5-01: 求下图中每个电容两端的电压
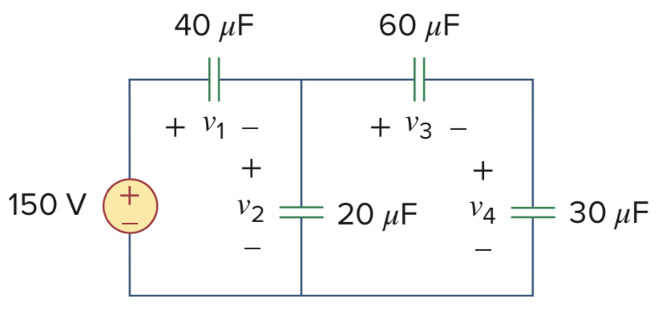
| 参考答案 | |
|---|---|
| SPICE仿真 | 仿真文件见 Github spice/ch02/CH02-KP5-01.kicad_sch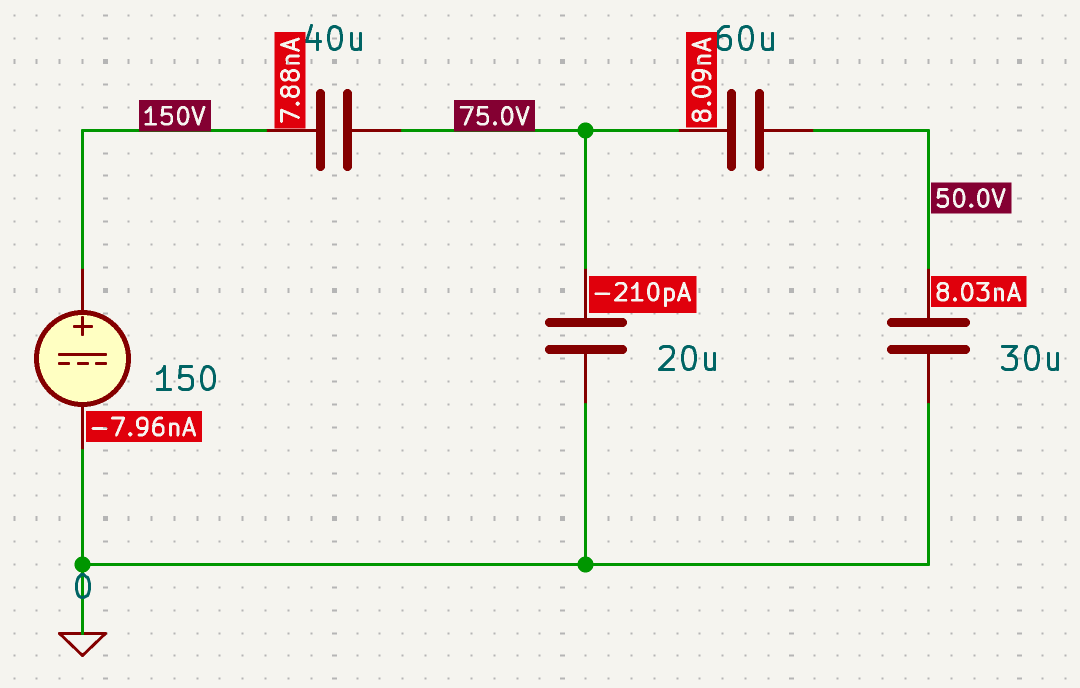 |
解析:
CH02-KP5-02: 求下图中的电容电压、电感电流,以及电容电压的储能
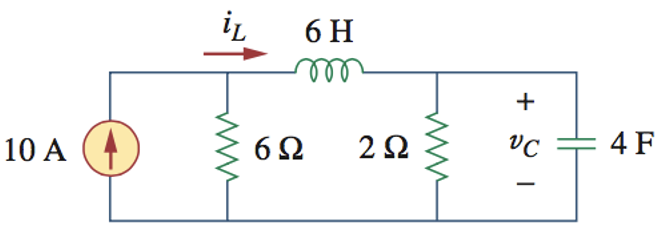
| 参考答案 | |
|---|---|
| SPCICE仿真 | 仿真文件见 Github spice/ch02/CH02-KP5-02.asc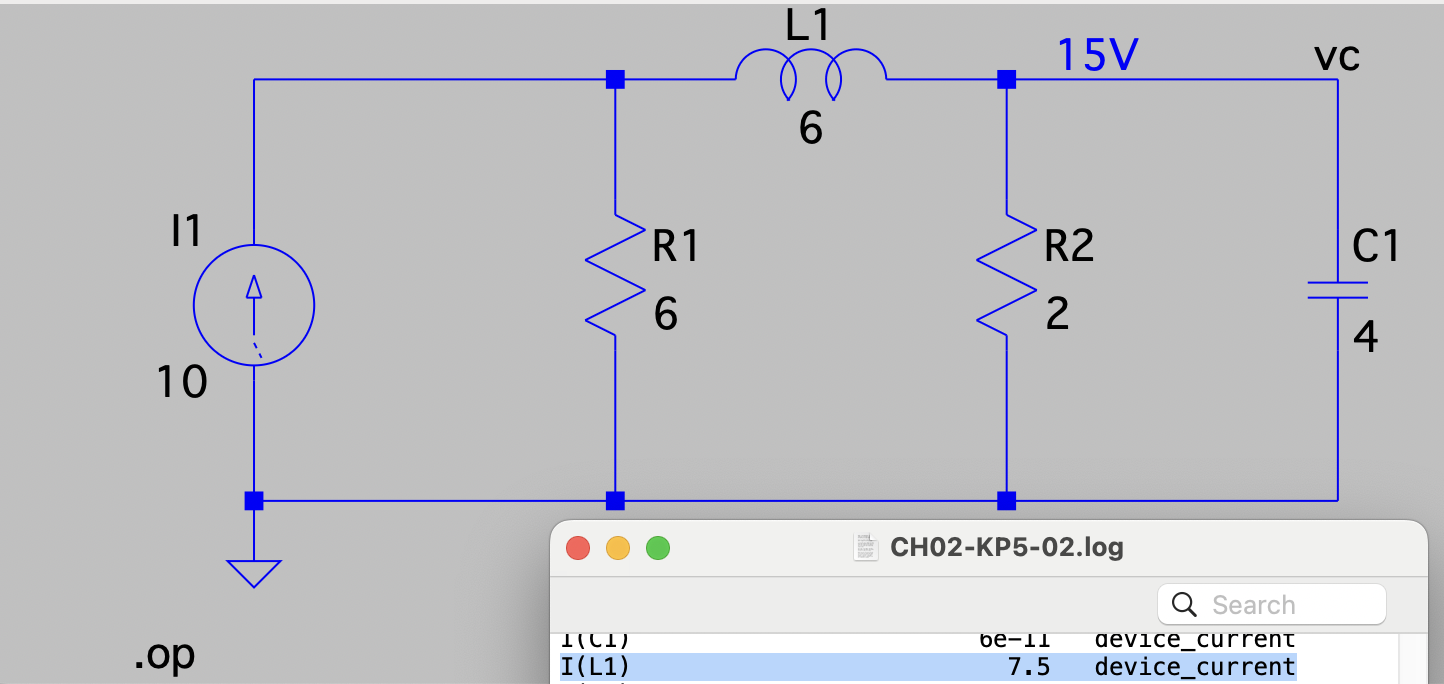 注意:LTspice 里的电感默认有 1 mΩ 的串联电阻,需要设置串联电阻值为 0,以覆盖默认值;Windows 版本的 LTspice 可以在电路图上标注元件电流,Mac 版本需要通过 log 查看。 |
解析:
知识点6:电源变换
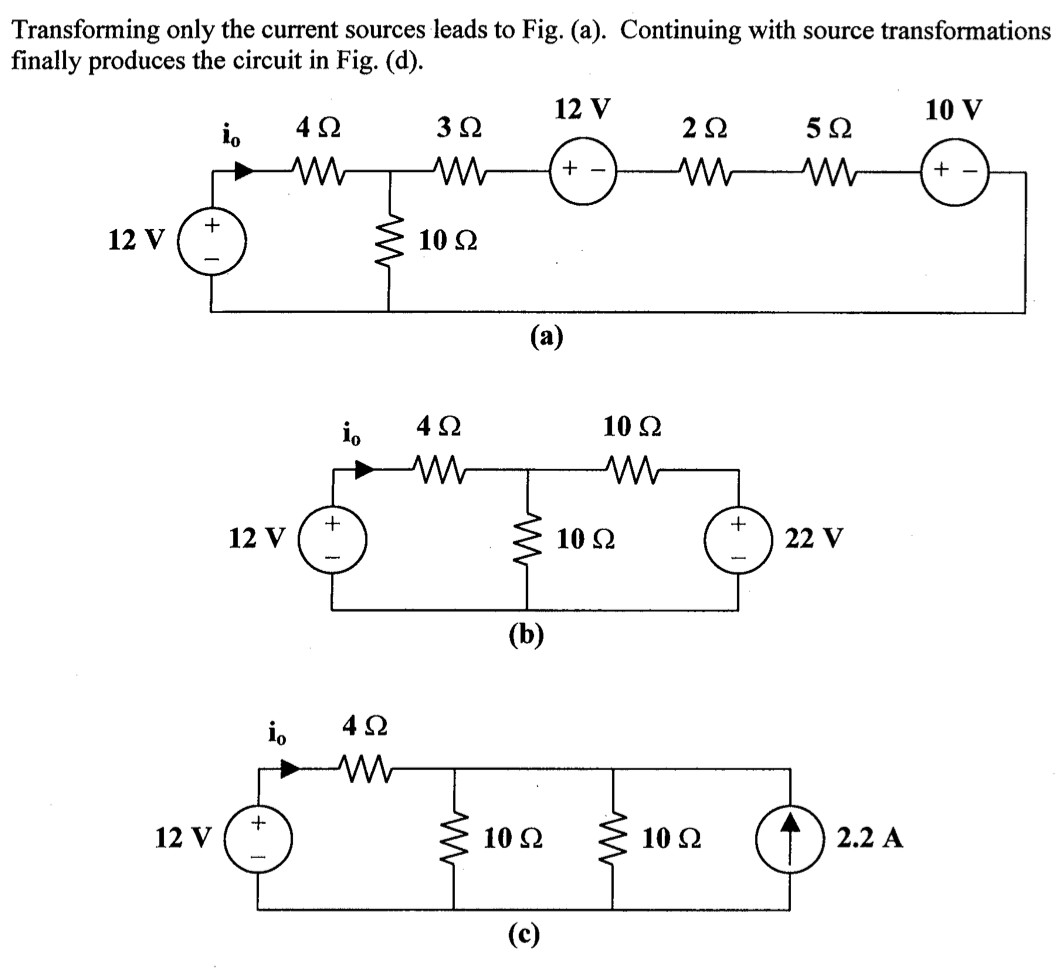
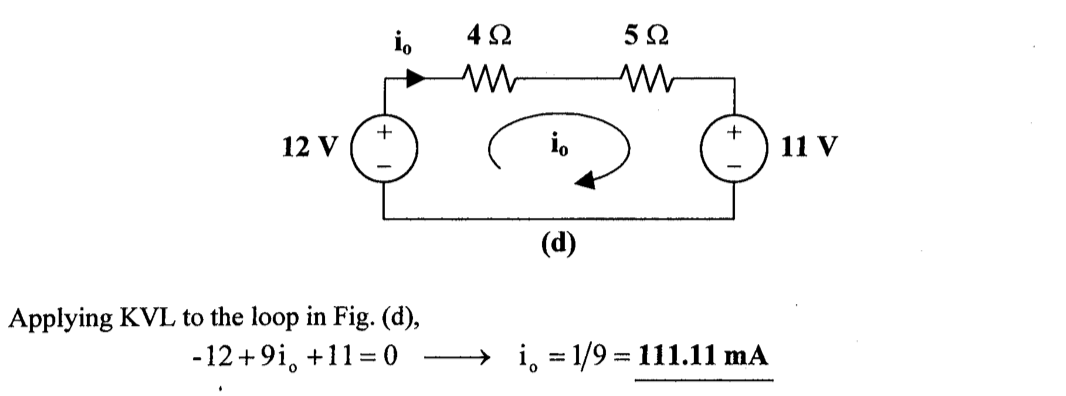
CH02-KP6-01: 采用电源变化,求下图中的
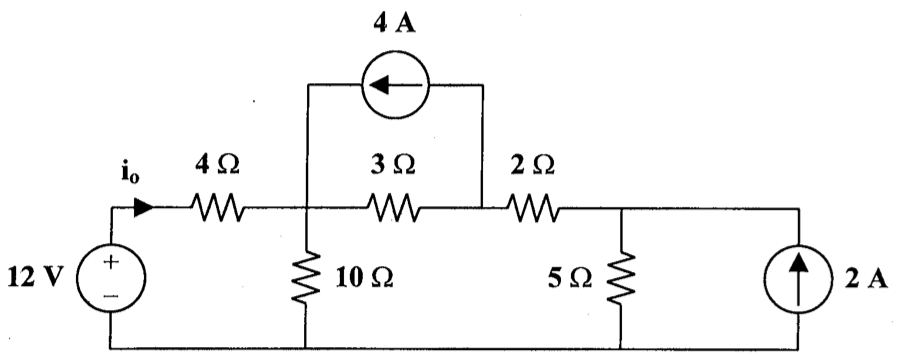
| 参考答案 | 111 mA |
|---|---|
| SPICE仿真 | 仿真文件见 Github spice/ch02/CH02-KP6-01.kicad_sch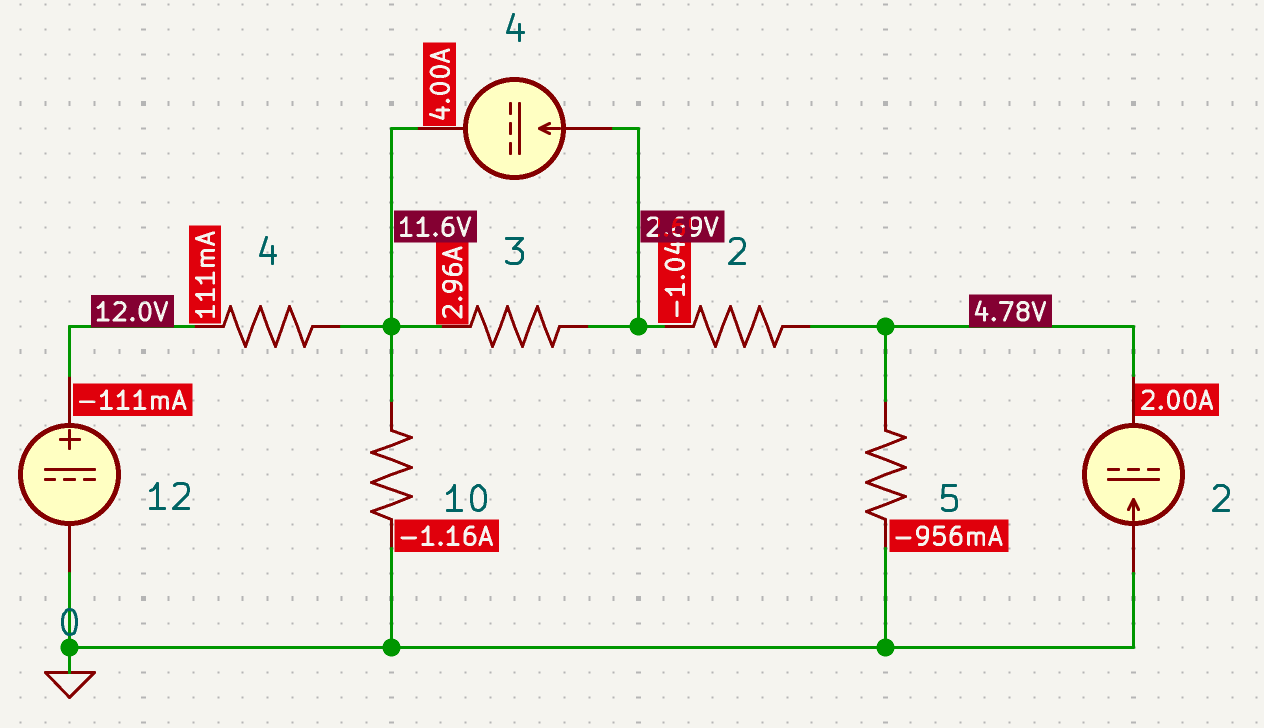 |
解析: